Question Number 168367 by MdNafiz last updated on 09/Apr/22

$$\mathrm{91}{x}^{\mathrm{2}} +\mathrm{84}{y}^{\mathrm{2}} −\mathrm{24}{xy}+\mathrm{406}{x}−\mathrm{392}{y}+\mathrm{799}=\mathrm{0} \\ $$$${find}\:{the}\:{eccentricity},{focus},{length}\:{of}\:{major}\:\&\:{minor}\:{axis},{directrix}\:\&\:{length}\:{of}\:{eccentric}\:{perpendicular} \\ $$$$ \\ $$
Answered by mr W last updated on 10/Apr/22
![91x^2 −2(12y−203)x+84y^2 −392y+799=0 Δ=(12y−203)^2 −91(84y^2 −392y+799)≥0 75y^2 −308y+315≤0 ((154−(√(91)))/(75))≤y≤((154+(√(91)))/(75)) ⇒y_C =((154)/(75)) 84y^2 −2(12x+196)y+91x^2 +406x+799=0 Δ=(12x+196)^2 −84(91x^2 +406x+799)≥0 75x^2 +294x+287≤0 ((−147−2(√(21)))/(75))≤x≤((−147+2(√(21)))/(75)) ⇒x_C =−((147)/(75)) x=−((147)/(75))+ρ cos θ y=((154)/(75))+ρ sin θ 91(−((147)/(75))+ρ cos θ)^2 +84(((154)/(75))+ρ sin θ)^2 −24(−((147)/(75))+ρ cos θ)(((154)/(75))+ρ sin θ)+406(−((147)/(75))+ρ cos θ)−392(((154)/(75))+ρ sin θ)+799=0 (175+7 cos 2θ−24 sin 2θ)ρ^2 −(8/3)=0 ρ^2 =(8/(3(175+7 cos 2θ−24 sin 2θ))) ρ^2 =(8/(3[175+25((7/(25)) cos 2θ−((24)/(25)) sin 2θ)])) ρ^2 =(8/(75[7−sin (2θ−tan^(−1) (7/(24)))])) ρ_(max) ^2 =(8/(75(7−1))) ⇒ρ_(max) =(2/(15))=semi major axis a at 2θ−tan^(−1) (7/(24))=(π/2) or θ_1 =(π/4)+(1/2)tan^(−1) (7/(24)) ρ_(min) ^2 =(8/(75(7+1))) ⇒ρ_(min) =((2(√6))/(45))=semi minor axis b at 2θ−tan^(−1) (7/(24))=−(π/2) or θ_2 =−(π/4)+(1/2)tan^(−1) (7/(24)) tan θ_1 =(4/3) tan θ_2 =−(3/4) ...](https://www.tinkutara.com/question/Q168414.png)
$$\mathrm{91}{x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{12}{y}−\mathrm{203}\right){x}+\mathrm{84}{y}^{\mathrm{2}} −\mathrm{392}{y}+\mathrm{799}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{12}{y}−\mathrm{203}\right)^{\mathrm{2}} −\mathrm{91}\left(\mathrm{84}{y}^{\mathrm{2}} −\mathrm{392}{y}+\mathrm{799}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{75}{y}^{\mathrm{2}} −\mathrm{308}{y}+\mathrm{315}\leqslant\mathrm{0} \\ $$$$\frac{\mathrm{154}−\sqrt{\mathrm{91}}}{\mathrm{75}}\leqslant{y}\leqslant\frac{\mathrm{154}+\sqrt{\mathrm{91}}}{\mathrm{75}} \\ $$$$\Rightarrow{y}_{{C}} =\frac{\mathrm{154}}{\mathrm{75}} \\ $$$$\mathrm{84}{y}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{12}{x}+\mathrm{196}\right){y}+\mathrm{91}{x}^{\mathrm{2}} +\mathrm{406}{x}+\mathrm{799}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{12}{x}+\mathrm{196}\right)^{\mathrm{2}} −\mathrm{84}\left(\mathrm{91}{x}^{\mathrm{2}} +\mathrm{406}{x}+\mathrm{799}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{75}{x}^{\mathrm{2}} +\mathrm{294}{x}+\mathrm{287}\leqslant\mathrm{0} \\ $$$$\frac{−\mathrm{147}−\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{75}}\leqslant{x}\leqslant\frac{−\mathrm{147}+\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{75}} \\ $$$$\Rightarrow{x}_{{C}} =−\frac{\mathrm{147}}{\mathrm{75}} \\ $$$${x}=−\frac{\mathrm{147}}{\mathrm{75}}+\rho\:\mathrm{cos}\:\theta \\ $$$${y}=\frac{\mathrm{154}}{\mathrm{75}}+\rho\:\mathrm{sin}\:\theta \\ $$$$\mathrm{91}\left(−\frac{\mathrm{147}}{\mathrm{75}}+\rho\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mathrm{84}\left(\frac{\mathrm{154}}{\mathrm{75}}+\rho\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} −\mathrm{24}\left(−\frac{\mathrm{147}}{\mathrm{75}}+\rho\:\mathrm{cos}\:\theta\right)\left(\frac{\mathrm{154}}{\mathrm{75}}+\rho\:\mathrm{sin}\:\theta\right)+\mathrm{406}\left(−\frac{\mathrm{147}}{\mathrm{75}}+\rho\:\mathrm{cos}\:\theta\right)−\mathrm{392}\left(\frac{\mathrm{154}}{\mathrm{75}}+\rho\:\mathrm{sin}\:\theta\right)+\mathrm{799}=\mathrm{0} \\ $$$$\left(\mathrm{175}+\mathrm{7}\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{24}\:\mathrm{sin}\:\mathrm{2}\theta\right)\rho^{\mathrm{2}} −\frac{\mathrm{8}}{\mathrm{3}}=\mathrm{0} \\ $$$$\rho^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{3}\left(\mathrm{175}+\mathrm{7}\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{24}\:\mathrm{sin}\:\mathrm{2}\theta\right)} \\ $$$$\rho^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{3}\left[\mathrm{175}+\mathrm{25}\left(\frac{\mathrm{7}}{\mathrm{25}}\:\mathrm{cos}\:\mathrm{2}\theta−\frac{\mathrm{24}}{\mathrm{25}}\:\mathrm{sin}\:\mathrm{2}\theta\right)\right]} \\ $$$$\rho^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{75}\left[\mathrm{7}−\mathrm{sin}\:\left(\mathrm{2}\theta−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{24}}\right)\right]} \\ $$$$\rho_{{max}} ^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{75}\left(\mathrm{7}−\mathrm{1}\right)} \\ $$$$\Rightarrow\rho_{{max}} =\frac{\mathrm{2}}{\mathrm{15}}={semi}\:{major}\:{axis}\:{a} \\ $$$${at}\:\mathrm{2}\theta−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{24}}=\frac{\pi}{\mathrm{2}}\:{or}\:\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{24}} \\ $$$$\rho_{{min}} ^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{75}\left(\mathrm{7}+\mathrm{1}\right)} \\ $$$$\Rightarrow\rho_{{min}} =\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{45}}={semi}\:{minor}\:{axis}\:{b}\: \\ $$$${at}\:\mathrm{2}\theta−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{24}}=−\frac{\pi}{\mathrm{2}}\:{or}\:\theta_{\mathrm{2}} =−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{24}} \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\theta_{\mathrm{2}} =−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$… \\ $$
Commented by Tawa11 last updated on 10/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 10/Apr/22
Commented by mr W last updated on 10/Apr/22
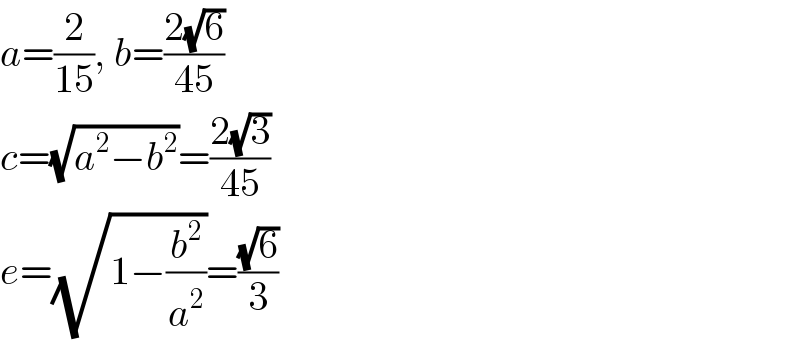
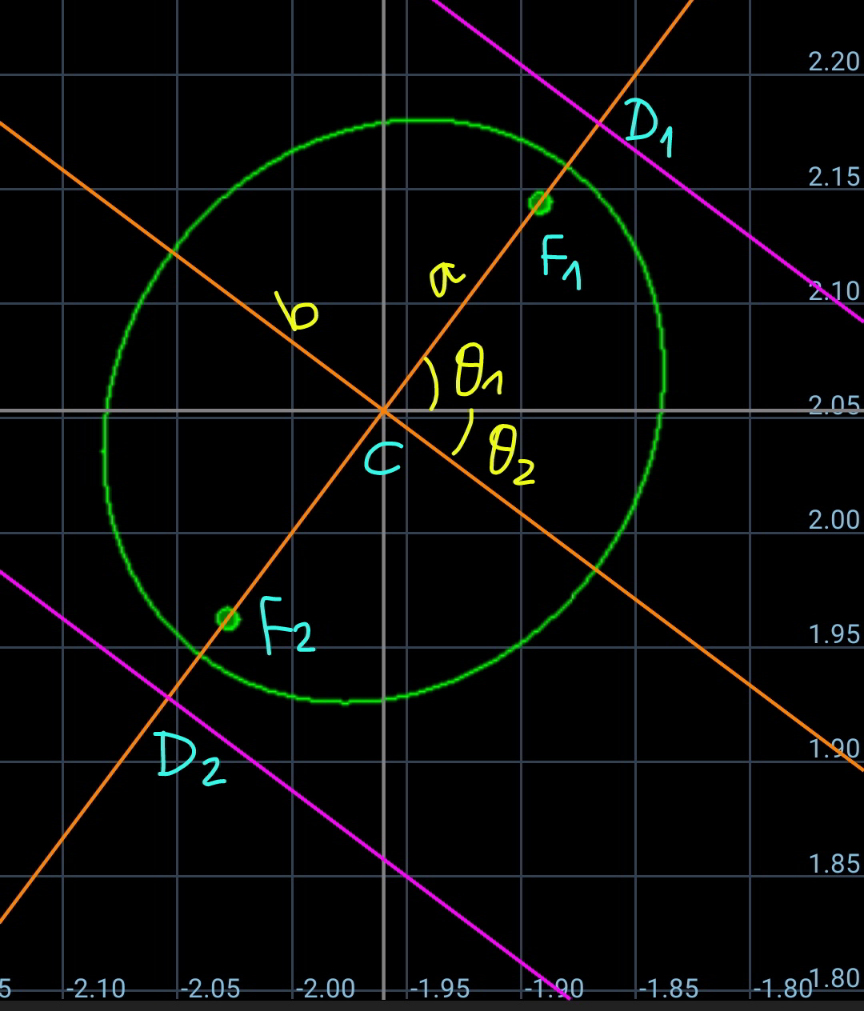
$${a}=\frac{\mathrm{2}}{\mathrm{15}},\:{b}=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{45}} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{45}} \\ $$$${e}=\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$
