Question Number 105207 by Anindita last updated on 26/Jul/20

$$\mathrm{99}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}}\:=\:? \\ $$$$\boldsymbol{{Can}}\:\boldsymbol{{you}}\:\boldsymbol{{solve}}\:\boldsymbol{{this}}? \\ $$
Commented by qwerty111 last updated on 26/Jul/20
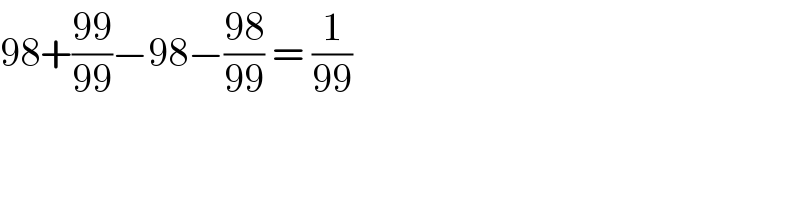
$$\mathrm{98}+\frac{\mathrm{99}}{\mathrm{99}}−\mathrm{98}−\frac{\mathrm{98}}{\mathrm{99}}\:=\:\frac{\mathrm{1}}{\mathrm{99}} \\ $$
Commented by JDamian last updated on 26/Jul/20
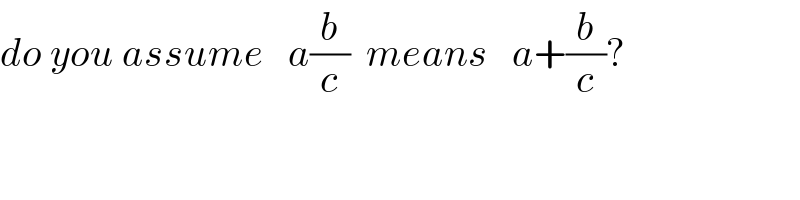
$${do}\:{you}\:{assume}\:\:\:{a}\frac{{b}}{{c}}\:\:{means}\:\:\:{a}+\frac{{b}}{{c}}? \\ $$
Commented by JDamian last updated on 27/Jul/20
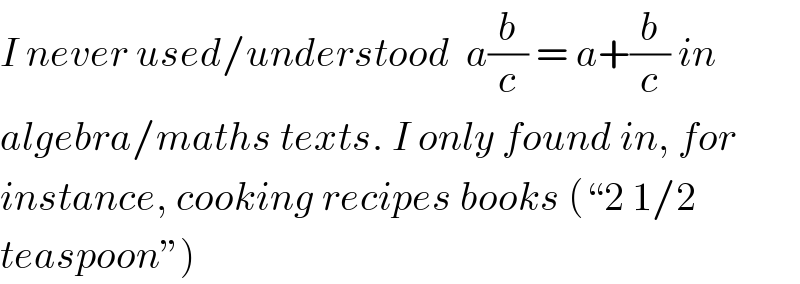
$${I}\:{never}\:{used}/{understood}\:\:{a}\frac{{b}}{{c}}\:=\:{a}+\frac{{b}}{{c}}\:{in} \\ $$$${algebra}/{maths}\:{texts}.\:{I}\:{only}\:{found}\:{in},\:{for} \\ $$$${instance},\:{cooking}\:{recipes}\:{books}\:\left(“\mathrm{2}\:\mathrm{1}/\mathrm{2}\right. \\ $$$$\left.{teaspoon}''\right) \\ $$
Answered by Aziztisffola last updated on 26/Jul/20
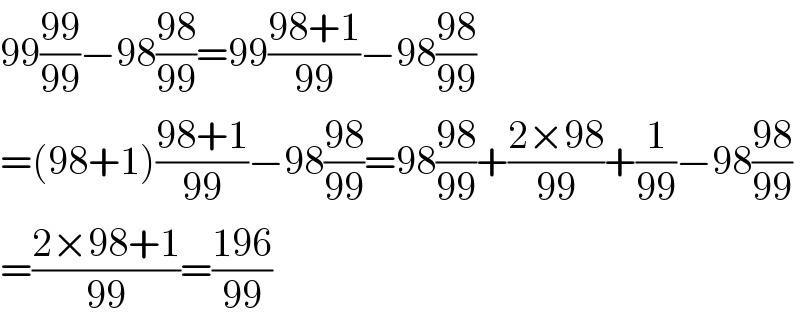
$$\mathrm{99}\frac{\mathrm{99}}{\mathrm{99}}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}}=\mathrm{99}\frac{\mathrm{98}+\mathrm{1}}{\mathrm{99}}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}} \\ $$$$=\left(\mathrm{98}+\mathrm{1}\right)\frac{\mathrm{98}+\mathrm{1}}{\mathrm{99}}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}}=\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}}+\frac{\mathrm{2}×\mathrm{98}}{\mathrm{99}}+\frac{\mathrm{1}}{\mathrm{99}}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}} \\ $$$$=\frac{\mathrm{2}×\mathrm{98}+\mathrm{1}}{\mathrm{99}}=\frac{\mathrm{196}}{\mathrm{99}} \\ $$
Commented by Aziztisffola last updated on 27/Jul/20
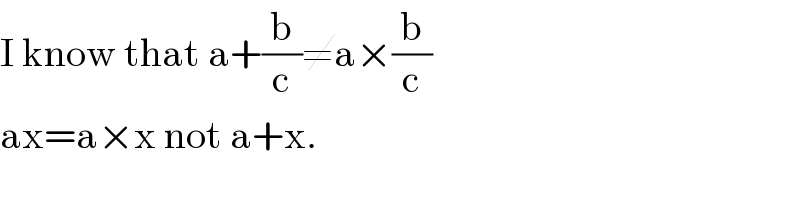
$$\mathrm{I}\:\mathrm{know}\:\mathrm{that}\:\mathrm{a}+\frac{\mathrm{b}}{\mathrm{c}}\neq\mathrm{a}×\frac{\mathrm{b}}{\mathrm{c}} \\ $$$$\mathrm{ax}=\mathrm{a}×\mathrm{x}\:\mathrm{not}\:\mathrm{a}+\mathrm{x}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 27/Jul/20
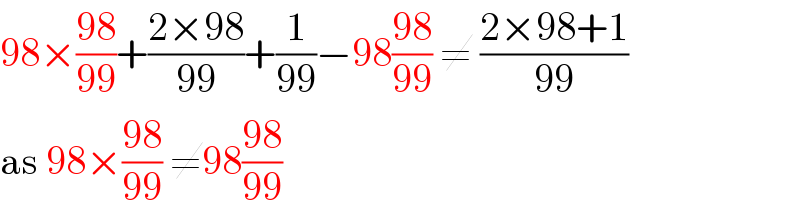
$$\mathrm{98}×\frac{\mathrm{98}}{\mathrm{99}}+\frac{\mathrm{2}×\mathrm{98}}{\mathrm{99}}+\frac{\mathrm{1}}{\mathrm{99}}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}}\:\neq\:\frac{\mathrm{2}×\mathrm{98}+\mathrm{1}}{\mathrm{99}} \\ $$$$\mathrm{as}\:\mathrm{98}×\frac{\mathrm{98}}{\mathrm{99}}\:\neq\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}} \\ $$
Commented by PRITHWISH SEN 2 last updated on 27/Jul/20
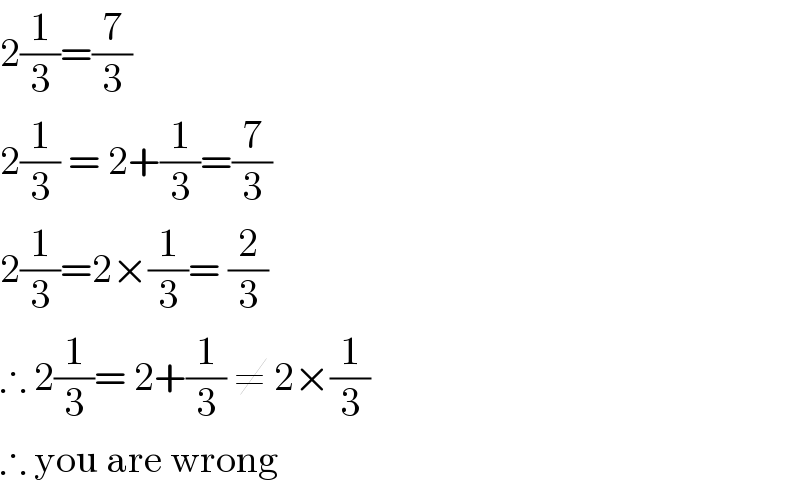
$$\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}}\:=\:\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\therefore\:\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}}=\:\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\:\neq\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\therefore\:\mathrm{you}\:\mathrm{are}\:\mathrm{wrong} \\ $$
Commented by qwerty111 last updated on 26/Jul/20

$$\:\bigstar\:\:\:\mathrm{98}\:\frac{\mathrm{98}+\mathrm{1}}{\mathrm{99}\:}\:\:\:\bigstar \\ $$
Commented by Aziztisffola last updated on 26/Jul/20

$$\mathrm{Just}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{calculus}. \\ $$
Commented by qwerty111 last updated on 26/Jul/20

$$\boldsymbol{{Ok}} \\ $$
Commented by Aziztisffola last updated on 26/Jul/20

$$\mathrm{I}\:\mathrm{assume}\:\mathrm{a}\frac{\mathrm{b}}{\mathrm{c}}=\mathrm{a}×\frac{\mathrm{b}}{\mathrm{c}}\:\mathrm{not}\:\mathrm{a}+\frac{\mathrm{b}}{\mathrm{c}} \\ $$
