Menu Close

9a-2-1-a-da-Evaluate-

Tinku Tara 0 Comments
Pin




Question Number 177400 by Mastermind last updated on 04/Oct/22
∫((√(9a^2 −1))/a)da Evaluate
$$\int\frac{\sqrt{\mathrm{9a}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{a}}\mathrm{da} \\ $$$$ \\ $$$$\mathrm{Evaluate} \\ $$
Commented by Frix last updated on 04/Oct/22
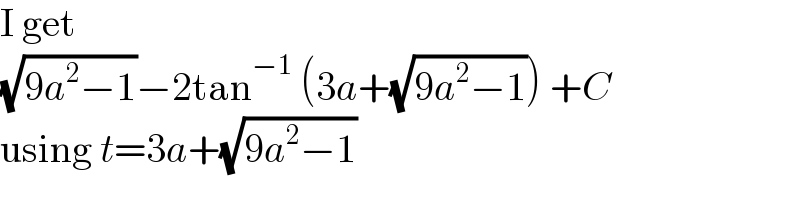
I get (√(9a^2 −1))−2tan^(−1) (3a+(√(9a^2 −1))) +C using t=3a+(√(9a^2 −1))
$$\mathrm{I}\:\mathrm{get} \\ $$$$\sqrt{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2tan}^{−\mathrm{1}} \:\left(\mathrm{3}{a}+\sqrt{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{1}}\right)\:+{C} \\ $$$$\mathrm{using}\:{t}=\mathrm{3}{a}+\sqrt{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{1}} \\ $$
Commented by BaliramKumar last updated on 04/Oct/22
solution?
$${solution}? \\ $$
Answered by BaliramKumar last updated on 04/Oct/22
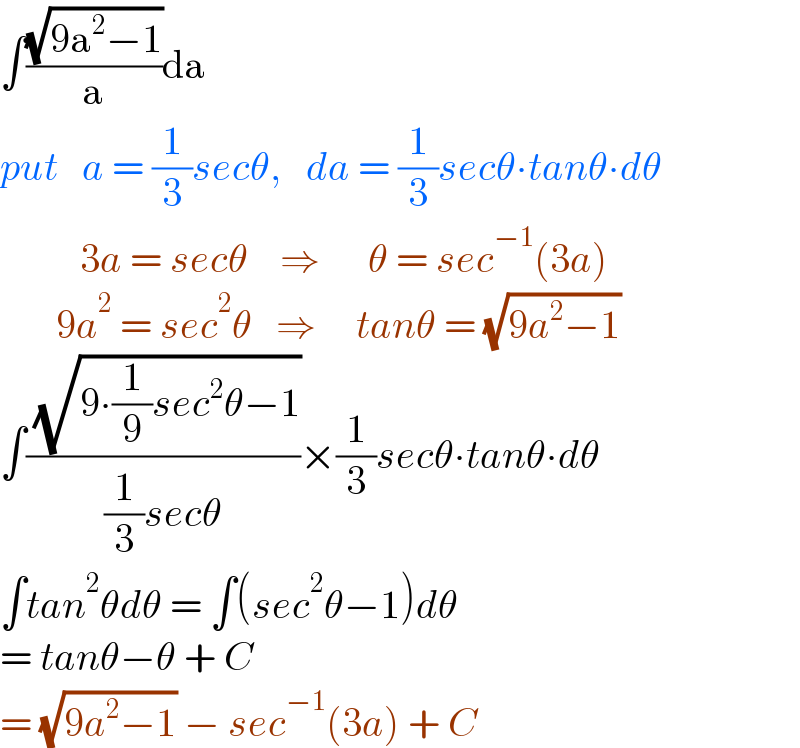
∫((√(9a^2 −1))/a)da put a = (1/3)secθ, da = (1/3)secθ∙tanθ∙dθ 3a = secθ ⇒ θ = sec^(−1) (3a) 9a^2 = sec^2 θ ⇒ tanθ = (√(9a^2 −1)) ∫(( (√(9∙(1/9)sec^2 θ−1)))/((1/3)secθ))×(1/3)secθ∙tanθ∙dθ ∫tan^2 θdθ = ∫(sec^2 θ−1)dθ = tanθ−θ + C = (√(9a^2 −1)) − sec^(−1) (3a) + C
$$\int\frac{\sqrt{\mathrm{9a}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{a}}\mathrm{da} \\ $$$${put}\:\:\:{a}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{sec}\theta,\:\:\:{da}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{sec}\theta\centerdot{tan}\theta\centerdot{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{3}{a}\:=\:{sec}\theta\:\:\:\:\Rightarrow\:\:\:\:\:\:\theta\:=\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{a}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{9}{a}^{\mathrm{2}} \:=\:{sec}^{\mathrm{2}} \theta\:\:\:\Rightarrow\:\:\:\:\:{tan}\theta\:=\:\sqrt{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\int\frac{\:\sqrt{\mathrm{9}\centerdot\frac{\mathrm{1}}{\mathrm{9}}{sec}^{\mathrm{2}} \theta−\mathrm{1}}}{\frac{\mathrm{1}}{\mathrm{3}}{sec}\theta}×\frac{\mathrm{1}}{\mathrm{3}}{sec}\theta\centerdot{tan}\theta\centerdot{d}\theta \\ $$$$\int{tan}^{\mathrm{2}} \theta{d}\theta\:=\:\int\left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right){d}\theta \\ $$$$=\:{tan}\theta−\theta\:+\:{C} \\ $$$$=\:\sqrt{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{1}}\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{a}\right)\:+\:{C} \\ $$
Answered by Ar Brandon last updated on 04/Oct/22
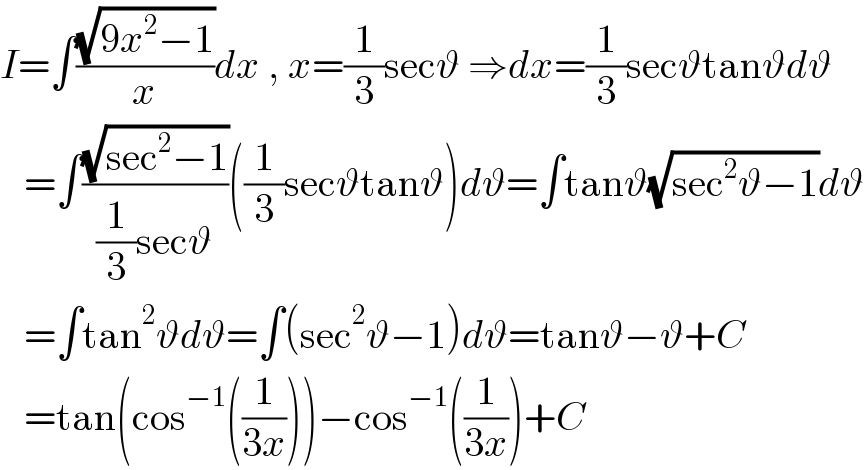
I=∫((√(9x^2 −1))/x)dx , x=(1/3)secϑ ⇒dx=(1/3)secϑtanϑdϑ =∫((√(sec^2 −1))/((1/3)secϑ))((1/3)secϑtanϑ)dϑ=∫tanϑ(√(sec^2 ϑ−1))dϑ =∫tan^2 ϑdϑ=∫(sec^2 ϑ−1)dϑ=tanϑ−ϑ+C =tan(cos^(−1) ((1/(3x))))−cos^(−1) ((1/(3x)))+C
$${I}=\int\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}{dx}\:,\:{x}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sec}\vartheta\:\Rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sec}\vartheta\mathrm{tan}\vartheta{d}\vartheta \\ $$$$\:\:\:=\int\frac{\sqrt{\mathrm{sec}^{\mathrm{2}} −\mathrm{1}}}{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sec}\vartheta}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sec}\vartheta\mathrm{tan}\vartheta\right){d}\vartheta=\int\mathrm{tan}\vartheta\sqrt{\mathrm{sec}^{\mathrm{2}} \vartheta−\mathrm{1}}{d}\vartheta \\ $$$$\:\:\:=\int\mathrm{tan}^{\mathrm{2}} \vartheta{d}\vartheta=\int\left(\mathrm{sec}^{\mathrm{2}} \vartheta−\mathrm{1}\right){d}\vartheta=\mathrm{tan}\vartheta−\vartheta+{C} \\ $$$$\:\:\:=\mathrm{tan}\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)\right)−\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)+{C} \\ $$
Answered by BaliramKumar last updated on 04/Oct/22
other approach I = ∫((√(9x^2 −1))/x)dx = ∫(√((9x^2 −1)/x^2 ))dx I = ∫(√(9−(1/x^2 )))dx = ∫(√(3^2 − ((1/x))^2 )) dx let (1/x) = 3sinθ, ((−1)/x^2 )dx = 3cosθdθ −9sin^2 θdx = 3cosθdθ I = ∫(√(9−9sin^2 θ))(− ((3cosθ)/(9sin^2 θ)))dθ I = −∫cot^2 θdθ = ∫(1−cosec^2 θ)dθ I = θ + cotθ + C I = sin^(−1) ((1/(3x))) + cot[sin^(−1) ((1/(3x)))] + C ■Answer I = cosec^(−1) (3x) + cot[cosec^(−1) (3x)] + C ■Answer I = (π/2) − sec^(−1) (3x) + cot[(π/2) − sec^(−1) (3x)] + c I = − sec^(−1) (3x) + tan[sec^(−1) (3x)] + c + (π/2) I = tan[sec^(−1) (3x)] − sec^(−1) (3x) + K ■Answer I = tan[tan^(−1) ((√(9x^2 −1)))] − sec^(−1) (3x) + K I = (√(9x^2 − 1 )) − sec^(−1) (3x) + K ■Answer
$${other}\:{approach} \\ $$$${I}\:=\:\int\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}\mathrm{d}{x}\:=\:\int\sqrt{\frac{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$${I}\:=\:\int\sqrt{\mathrm{9}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx}\:=\:\int\sqrt{\mathrm{3}^{\mathrm{2}} \:−\:\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }\:{dx} \\ $$$${let}\:\:\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{3}{sin}\theta,\:\:\:\frac{−\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:=\:\mathrm{3}{cos}\theta{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{9}{sin}^{\mathrm{2}} \theta{dx}\:=\:\mathrm{3}{cos}\theta{d}\theta \\ $$$${I}\:=\:\int\sqrt{\mathrm{9}−\mathrm{9}{sin}^{\mathrm{2}} \theta}\left(−\:\frac{\mathrm{3}{cos}\theta}{\mathrm{9}{sin}^{\mathrm{2}} \theta}\right){d}\theta \\ $$$${I}\:=\:−\int{cot}^{\mathrm{2}} \theta{d}\theta\:=\:\int\left(\mathrm{1}−{cosec}^{\mathrm{2}} \theta\right){d}\theta \\ $$$${I}\:=\:\theta\:+\:{cot}\theta\:+\:{C} \\ $$$${I}\:=\:{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)\:+\:{cot}\left[{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)\right]\:+\:{C}\:\:\:\:\:\blacksquare{Answer} \\ $$$${I}\:=\:{cosec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\:+\:{cot}\left[{cosec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\right]\:+\:{C}\:\:\:\blacksquare{Answer} \\ $$$${I}\:=\:\frac{\pi}{\mathrm{2}}\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\:+\:{cot}\left[\frac{\pi}{\mathrm{2}}\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\right]\:+\:{c} \\ $$$${I}\:=\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\:+\:{tan}\left[{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\right]\:+\:{c}\:+\:\frac{\pi}{\mathrm{2}} \\ $$$${I}\:=\:{tan}\left[{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\right]\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\:+\:{K}\:\:\:\:\:\:\:\blacksquare{Answer} \\ $$$${I}\:=\:{tan}\left[{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}}\right)\right]\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\:+\:{K} \\ $$$${I}\:=\:\sqrt{\mathrm{9}{x}^{\mathrm{2}} \:−\:\mathrm{1}\:}\:−\:{sec}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)\:+\:{K}\:\:\:\:\:\:\blacksquare{Answer} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *