Question Number 96007 by 6532 last updated on 29/May/20
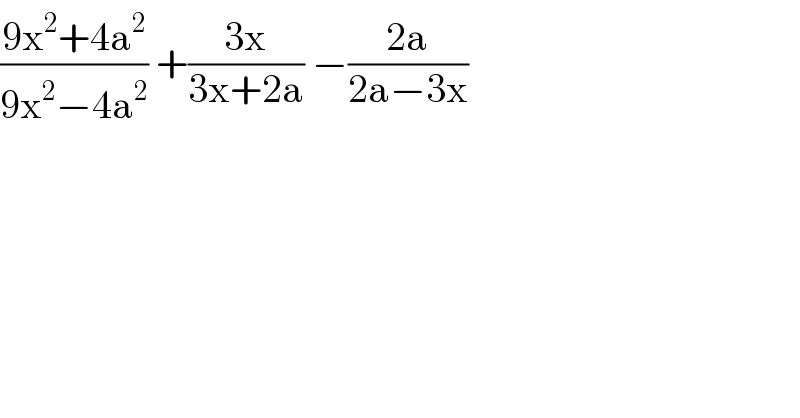
$$\frac{\mathrm{9x}^{\mathrm{2}} +\mathrm{4a}^{\mathrm{2}} }{\mathrm{9x}^{\mathrm{2}} −\mathrm{4a}^{\mathrm{2}} }\:+\frac{\mathrm{3x}}{\mathrm{3x}+\mathrm{2a}}\:−\frac{\mathrm{2a}}{\mathrm{2a}−\mathrm{3x}} \\ $$
Commented by i jagooll last updated on 29/May/20
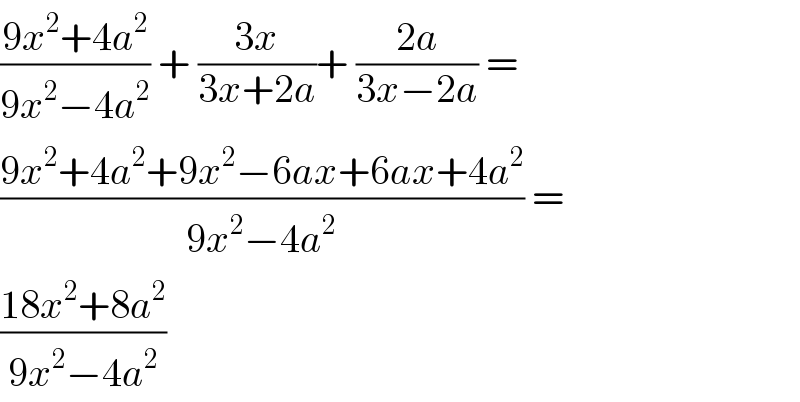
$$\frac{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} }\:+\:\frac{\mathrm{3}{x}}{\mathrm{3}{x}+\mathrm{2}{a}}+\:\frac{\mathrm{2}{a}}{\mathrm{3}{x}−\mathrm{2}{a}}\:=\: \\ $$$$\frac{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{6}{ax}+\mathrm{6}{ax}+\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} }\:= \\ $$$$\frac{\mathrm{18}{x}^{\mathrm{2}} +\mathrm{8}{a}^{\mathrm{2}} }{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} }\: \\ $$
