Question Number 161930 by Rasheed.Sindhi last updated on 24/Dec/21
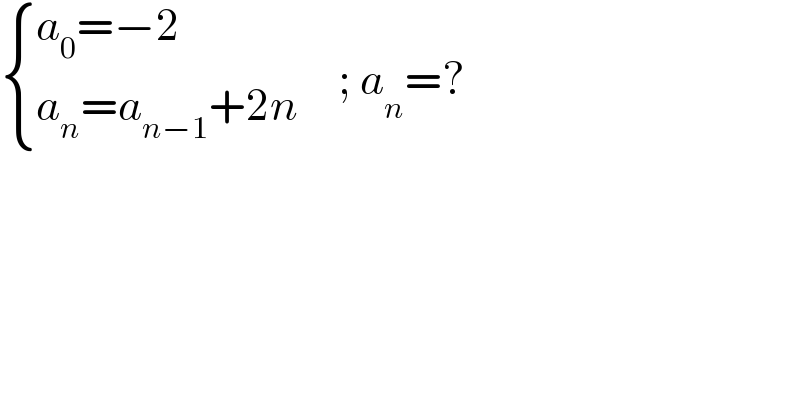
$$\begin{cases}{{a}_{\mathrm{0}} =−\mathrm{2}\:}\\{{a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{2}{n}}\end{cases}\:\:\:\:\:;\:{a}_{{n}} =? \\ $$
Answered by mr W last updated on 24/Dec/21
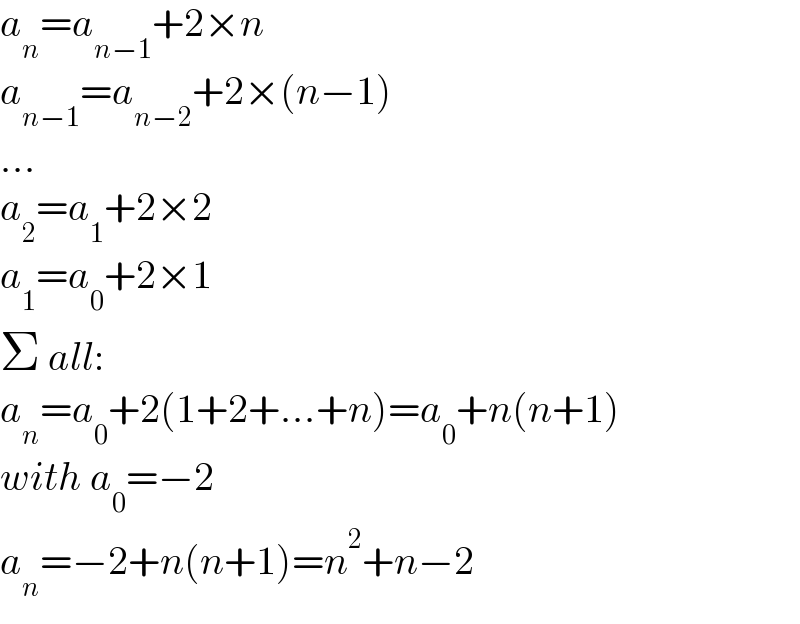
$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{2}×{n} \\ $$$${a}_{{n}−\mathrm{1}} ={a}_{{n}−\mathrm{2}} +\mathrm{2}×\left({n}−\mathrm{1}\right) \\ $$$$… \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}} +\mathrm{2}×\mathrm{2} \\ $$$${a}_{\mathrm{1}} ={a}_{\mathrm{0}} +\mathrm{2}×\mathrm{1} \\ $$$$\Sigma\:{all}: \\ $$$${a}_{{n}} ={a}_{\mathrm{0}} +\mathrm{2}\left(\mathrm{1}+\mathrm{2}+…+{n}\right)={a}_{\mathrm{0}} +{n}\left({n}+\mathrm{1}\right) \\ $$$${with}\:{a}_{\mathrm{0}} =−\mathrm{2} \\ $$$${a}_{{n}} =−\mathrm{2}+{n}\left({n}+\mathrm{1}\right)={n}^{\mathrm{2}} +{n}−\mathrm{2} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Dec/21

$$\mathcal{T}{han}\mathcal{X}\:\mathcal{S}{ir}! \\ $$
