Menu Close

a-0-4-1-tgx-dx-b-0-1-1-lnx-dx-

Tinku Tara 0 Comments
Pin




Question Number 61674 by behi83417@gmail.com last updated on 06/Jun/19
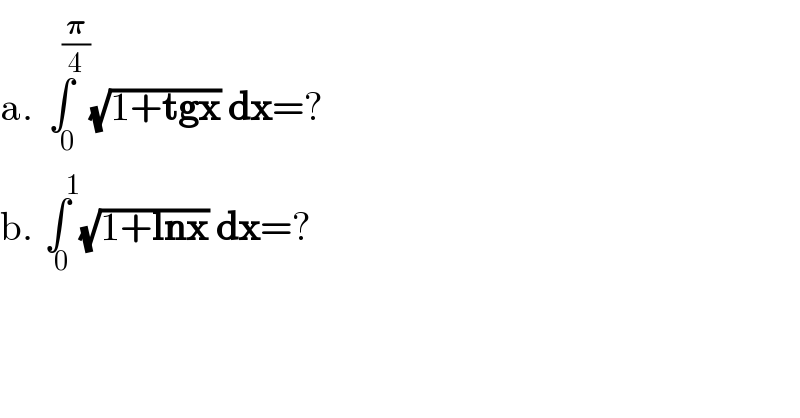
a.∫_( 0) ^( (𝛑/4)) (√(1+tgx)) dx=? b.∫_( 0) ^( 1) (√(1+lnx)) dx=?
$$\mathrm{a}.\underset{\:\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\frac{\boldsymbol{\pi}}{\mathrm{4}}} {\int}}\sqrt{\mathrm{1}+\boldsymbol{\mathrm{tgx}}}\:\boldsymbol{\mathrm{dx}}=? \\ $$$$\mathrm{b}.\underset{\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\:\mathrm{1}} {\int}}\sqrt{\mathrm{1}+\boldsymbol{\mathrm{lnx}}}\:\boldsymbol{\mathrm{dx}}=? \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
b) we must have 1+ln(x)>0 β‡’ln(x)>βˆ’1 =ln((1/e)) β‡’x>(1/e) so the fonction is not defined on]0,1] i think the Q is find ∫_0 ^1 (√(1βˆ’ln(x)))dx let use the chang (√(1βˆ’ln(x)))=t β‡’1βˆ’ln(x) =t^2 β‡’ln(x)=1βˆ’t^2 β‡’ x =e^(1βˆ’t^2 ) β‡’ ∫_0 ^1 (√(1βˆ’ln(x)))dx = ∫_(+∞) ^1 t (βˆ’2t)e^(1βˆ’t^2 ) dt = 2∫_1 ^(+∞) t^2 e^(1βˆ’t^2 ) dt =2e ∫_1 ^(+∞) t^2 e^(βˆ’t^2 ) dt by parts ∫_1 ^(+∞) t^2 e^(βˆ’t^2 ) dt =βˆ’(1/2)∫_1 ^(+∞) t(βˆ’2t)e^(βˆ’t^2 ) dt =βˆ’(1/2){ [t e^(βˆ’t^2 ) ]_1 ^(+∞) βˆ’βˆ«_1 ^(+∞) e^(βˆ’t^2 ) dt} =βˆ’(1/2){ βˆ’(1/e) βˆ’βˆ«_1 ^(+∞) e^(βˆ’t^2 ) dt} =(1/(2e)) +(1/2) ∫_1 ^(+∞) e^(βˆ’t^2 ) dt ∫_0 ^∞ e^(βˆ’t^2 ) dt =∫_0 ^1 e^(βˆ’t^2 ) dt +∫_1 ^(+∞) e^(βˆ’t^2 ) dt =((βˆšΟ€)/2) β‡’βˆ«_1 ^(+∞) e^(βˆ’t^2 ) dt=((βˆšΟ€)/2) βˆ’βˆ«_0 ^1 e^(βˆ’t^2 ) dt =((βˆšΟ€)/2) βˆ’Ξ£_(n=0) ^∞ (((βˆ’1)^n )/(n!))∫_0 ^1 t^(2n) dt β‡’ ∫_0 ^1 (√(1βˆ’ln(x)))dx =(1/(2e)) +((βˆšΟ€)/4) βˆ’(1/2) Ξ£_(n=0) ^∞ (((βˆ’1)^n )/(n!(2n+1))) approximate value is ∫_0 ^1 (√(1βˆ’ln(x)))dx ∼ (1/(2e)) +((βˆšΟ€)/4) βˆ’(1/2){ 1 βˆ’(1/3) +(1/(10)) βˆ’(1/(21))} β‡’ ∫_0 ^1 (√(1βˆ’ln(x)))dx ∼ (1/(2e)) +((βˆšΟ€)/4) βˆ’(1/2) +(1/6) βˆ’(1/(20)) +(1/(42)) .
$$\left.{b}\right)\:{we}\:{must}\:{have}\:\mathrm{1}+{ln}\left({x}\right)>\mathrm{0}\:\Rightarrow{ln}\left({x}\right)>βˆ’\mathrm{1}\:={ln}\left(\frac{\mathrm{1}}{{e}}\right)\:\Rightarrow{x}>\frac{\mathrm{1}}{{e}}\:\:{so}\:{the}\:{fonction} \\ $$$$\left.{i}\left.{s}\:{not}\:{defined}\:{on}\right]\mathrm{0},\mathrm{1}\right]\:\:\:\:{i}\:\:{think}\:{the}\:{Q}\:{is}\:{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}βˆ’{ln}\left({x}\right)}{dx} \\ $$$${let}\:{use}\:{the}\:{chang}\:\:\sqrt{\mathrm{1}βˆ’{ln}\left({x}\right)}={t}\:\Rightarrow\mathrm{1}βˆ’{ln}\left({x}\right)\:={t}^{\mathrm{2}} \:\Rightarrow{ln}\left({x}\right)=\mathrm{1}βˆ’{t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}\:={e}^{\mathrm{1}βˆ’{t}^{\mathrm{2}} } \:\:\:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}βˆ’{ln}\left({x}\right)}{dx}\:=\:\int_{+\infty} ^{\mathrm{1}} {t}\:\:\left(βˆ’\mathrm{2}{t}\right){e}^{\mathrm{1}βˆ’{t}^{\mathrm{2}} } {dt} \\ $$$$=\:\mathrm{2}\int_{\mathrm{1}} ^{+\infty} \:{t}^{\mathrm{2}} \:{e}^{\mathrm{1}βˆ’{t}^{\mathrm{2}} } {dt}\:=\mathrm{2}{e}\:\int_{\mathrm{1}} ^{+\infty} \:\:{t}^{\mathrm{2}} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\:\:\:{by}\:{parts}\: \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\:{t}^{\mathrm{2}} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\:\:=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{+\infty} \:{t}\left(βˆ’\mathrm{2}{t}\right){e}^{βˆ’{t}^{\mathrm{2}} } {dt}\:=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left[{t}\:{e}^{βˆ’{t}^{\mathrm{2}} } \right]_{\mathrm{1}} ^{+\infty} \:βˆ’\int_{\mathrm{1}} ^{+\infty} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\right\} \\ $$$$=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\left\{\:βˆ’\frac{\mathrm{1}}{{e}}\:βˆ’\int_{\mathrm{1}} ^{+\infty} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}{e}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{+\infty} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\:+\int_{\mathrm{1}} ^{+\infty} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow\int_{\mathrm{1}} ^{+\infty} \:\:{e}^{βˆ’{t}^{\mathrm{2}} } {dt}=\frac{\sqrt{\pi}}{\mathrm{2}}\:βˆ’\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{βˆ’{t}^{\mathrm{2}} } {dt} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\:βˆ’\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(βˆ’\mathrm{1}\right)^{{n}} }{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}{n}} {dt}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}βˆ’{ln}\left({x}\right)}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}{e}}\:+\frac{\sqrt{\pi}}{\mathrm{4}}\:βˆ’\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(βˆ’\mathrm{1}\right)^{{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${approximate}\:{value}\:{is} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}βˆ’{ln}\left({x}\right)}{dx}\:\sim\:\:\frac{\mathrm{1}}{\mathrm{2}{e}}\:+\frac{\sqrt{\pi}}{\mathrm{4}}\:βˆ’\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\mathrm{1}\:βˆ’\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{10}}\:βˆ’\frac{\mathrm{1}}{\mathrm{21}}\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}βˆ’{ln}\left({x}\right)}{dx}\:\sim\:\frac{\mathrm{1}}{\mathrm{2}{e}}\:+\frac{\sqrt{\pi}}{\mathrm{4}}\:βˆ’\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{6}}\:βˆ’\frac{\mathrm{1}}{\mathrm{20}}\:+\frac{\mathrm{1}}{\mathrm{42}}\:. \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 06/Jun/19
sir proph Abdo!thank you very much for so hard working.god bless you sir.
$$\mathrm{sir}\:\mathrm{proph}\:\mathrm{Abdo}!\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$$$\mathrm{for}\:\mathrm{so}\:\mathrm{hard}\:\mathrm{working}.\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
a)let I=∫_0 ^(Ο€/4) (√(1+tanx))dx changeent (√(1+tanx))=t give 1+tanx =t^2 β‡’tanx=t^2 βˆ’1 β‡’ x =arctan(t^2 βˆ’1) β‡’ I = ∫_1 ^(√2) (t/(1+(t^2 βˆ’1)^2 ))(2t) dt =2 ∫_1 ^(√2) (t^2 /(t^4 βˆ’2t^2 +2)) dt let decompose F(t) =(t^2 /(t^4 βˆ’2t^2 +2)) t^4 βˆ’2t^2 +2 =0 β‡’u^2 βˆ’2u +2 =0 (u=t^2 ) Ξ”^β€² =1βˆ’2=βˆ’1<0 β‡’ let Ξ»^4 =2 β‡’t^4 βˆ’2t^2 +2 =t^(4 ) +Ξ»^4 βˆ’2t^2 =(t^2 +Ξ»^2 )^2 βˆ’2Ξ»^2 t^2 βˆ’2t^2 =(t^2 +Ξ»^2 )^2 βˆ’2(1+Ξ»^2 )t^2 =(t^2 +Ξ»^2 βˆ’(√(2(1+Ξ»^2 )))t)(t^2 +Ξ»^2 +(√(2(1+Ξ»^2 )))t) β‡’ F(t) =((at +b)/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) +((ct +d)/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 )) (Ξ» =2^(1/4) ) F(βˆ’t)=F(t) β‡’c=βˆ’a and d=b β‡’ F(t) =((at +b)/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) +((βˆ’at +b)/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 )) F(0) =0 =((2b)/Ξ»^2 ) β‡’b=0 F(1) = 1 = (a/(Ξ»^2 +1βˆ’(√(2(1+Ξ»^2 )))) βˆ’(a/(Ξ»^2 +1+(√(2(1+Ξ»^2 ))))) β‡’ 2(√(2(1+Ξ»^2 )))a =1 β‡’ a =(1/(2(√(2(1+Ξ»^2 ))))) β‡’ ∫_1 ^(√2) F(t)dt =(1/(2(√(2(1+Ξ»^2 ))))){ ∫_1 ^(√2) ((tdt)/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) βˆ’βˆ«_1 ^(√2) ((tdt)/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 ))} ∫_1 ^(√2) ((tdt)/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) =(1/2) ∫_1 ^(√2) ((2tβˆ’(√(2(1+Ξ»^2 ))) +(√(2(1+Ξ»^2 ))))/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) dt ∫_1 ^(√2) ((tdt)/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 )) =(1/2) ∫_1 ^(√2) ((2t +(√(2(1+Ξ»^2 ))) βˆ’(√(2(1+Ξ»^2 ))))/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 )) dt β‡’ ∫_1 ^(√2) F(t)dt = (1/(2(√(2(1+Ξ»^2 ))))){ [ln∣((t^2 βˆ’(√(2(1+Ξ»^2 )))t +1)/(t^2 +(√(2(1+Ξ»^2 )))))∣_1 ^(√2) +((√(2(1+Ξ»^2 )))/2) ∫_1 ^(√2) (dt/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) +((√(2(1+Ξ»^2 )))/2) ∫_1 ^(√2) (dt/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 )) ∫_1 ^(√2) (dt/(t^2 βˆ’(√(2(1+Ξ»^2 )))t +Ξ»^2 )) =∫_1 ^(√2) (dt/(t^2 βˆ’2 ((√(2(1+Ξ»^2 )))/2)t +(1/2)(1+Ξ»^2 )+Ξ»^2 βˆ’(1/2)(1+Ξ»^2 ))) =∫_1 ^(√2) (dt/((tβˆ’((√(2(1+Ξ»^2 )))/2))^2 +((Ξ»^2 βˆ’1)/2))) (Ξ»^2 βˆ’1=(√2)βˆ’1>) =_(tβˆ’((√(2(1+Ξ»^2 )))/2)=(√((Ξ»^2 βˆ’1)/2))u) ∫_((2βˆ’(√(2(1+Ξ»^2 ))))/(2(√((Ξ»^2 βˆ’1)/2)))) ^((2(√2)βˆ’(√(2(1+Ξ»^2 ))))/(2(√((Ξ»^2 βˆ’1)/2)))) (1/(((Ξ»^2 βˆ’1)/2)(1+u^2 ))) (√((Ξ»^2 βˆ’1)/2))du =(√(2/(Ξ»^2 βˆ’1))) { arctan(((2(√2)βˆ’(√(2(1+Ξ»^2 ))))/(2(√((Ξ»^2 βˆ’1)/2)))))βˆ’arctan(((2βˆ’(√(2(1+Ξ»^2 ))))/(2(√((Ξ»^2 βˆ’1)/2)))))} =(√(2/( (√2)βˆ’1))){ arctan(((2(√2)βˆ’(√(2(1+(√2)))))/(2(√(((√2)βˆ’1)/2)))))βˆ’arctan(((2βˆ’(√(2(1+(√2)))))/(2(√(((√2)βˆ’1)/2)))))}alsl ∫_1 ^(√2) (dt/(t^2 +(√(2(1+Ξ»^2 )))t +Ξ»^2 )) =_(t =βˆ’x) ∫_(βˆ’1) ^(βˆ’(√2)) ((βˆ’dx)/(x^2 βˆ’(√(2(1+Ξ»^2 )))x +Ξ»^2 )) =βˆ’βˆ«_(βˆ’1) ^(βˆ’(√2)) (dx/(x^2 βˆ’(√(2(1+Ξ»^2 )))x+Ξ»^2 )) =.....
$$\left.{a}\right){let}\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+{tanx}}{dx}\:{changeent}\:\sqrt{\mathrm{1}+{tanx}}={t}\:{give}\:\mathrm{1}+{tanx}\:={t}^{\mathrm{2}} \:\Rightarrow{tanx}={t}^{\mathrm{2}} βˆ’\mathrm{1}\:\Rightarrow \\ $$$${x}\:={arctan}\left({t}^{\mathrm{2}} βˆ’\mathrm{1}\right)\:\Rightarrow\:{I}\:=\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{t}}{\mathrm{1}+\left({t}^{\mathrm{2}} βˆ’\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{2}{t}\right)\:{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} βˆ’\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}\:{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} βˆ’\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}} \\ $$$${t}^{\mathrm{4}} βˆ’\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}\:=\mathrm{0}\:\Rightarrow{u}^{\mathrm{2}} βˆ’\mathrm{2}{u}\:+\mathrm{2}\:=\mathrm{0}\:\:\:\left({u}={t}^{\mathrm{2}} \right) \\ $$$$\Delta^{'} \:=\mathrm{1}βˆ’\mathrm{2}=βˆ’\mathrm{1}<\mathrm{0}\:\:\Rightarrow\:{let}\:\lambda^{\mathrm{4}} \:=\mathrm{2}\:\Rightarrow{t}^{\mathrm{4}} βˆ’\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}\:={t}^{\mathrm{4}\:} +\lambda^{\mathrm{4}} βˆ’\mathrm{2}{t}^{\mathrm{2}} \\ $$$$=\left({t}^{\mathrm{2}} +\lambda^{\mathrm{2}} \right)^{\mathrm{2}} βˆ’\mathrm{2}\lambda^{\mathrm{2}} {t}^{\mathrm{2}} βˆ’\mathrm{2}{t}^{\mathrm{2}} \:=\left({t}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} \right)^{\mathrm{2}} \:βˆ’\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right){t}^{\mathrm{2}} \\ $$$$\left.=\left({t}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\right)\left({t}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} +\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right.}\right){t}\right)\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{\left.{t}^{\mathrm{2}} +\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right.}\right){t}\:+\lambda^{\mathrm{2}} }\:\:\:\:\:\:\left(\lambda\:=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \right) \\ $$$${F}\left(βˆ’{t}\right)={F}\left({t}\right)\:\Rightarrow{c}=βˆ’{a}\:{and}\:{d}={b}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:+\frac{βˆ’{at}\:+{b}}{\left.{t}^{\mathrm{2}} +\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right.}\right){t}\:+\lambda^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\frac{\mathrm{2}{b}}{\lambda^{\mathrm{2}} }\:\Rightarrow{b}=\mathrm{0} \\ $$$${F}\left(\mathrm{1}\right)\:=\:\mathrm{1}\:=\:\frac{{a}}{\lambda^{\mathrm{2}} \:+\mathrm{1}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right.}}\:βˆ’\frac{{a}}{\lambda^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}\:\Rightarrow \\ $$$$\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{a}\:=\mathrm{1}\:\Rightarrow\:{a}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:{F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}\left\{\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{tdt}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:βˆ’\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{tdt}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\right\} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{tdt}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{\mathrm{2}{t}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}\:+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:{dt} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{tdt}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{\mathrm{2}{t}\:+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}\:βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:{dt}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:{F}\left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}\left\{\:\:\left[{ln}\mid\frac{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\mathrm{1}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}\mid_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \right.\right. \\ $$$$+\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:+\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} } \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} βˆ’\mathrm{2}\:\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}}{t}\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)+\lambda^{\mathrm{2}} βˆ’\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\:\:\:\frac{{dt}}{\left({t}βˆ’\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}\:\:\:\:\:\left(\lambda^{\mathrm{2}} βˆ’\mathrm{1}=\sqrt{\mathrm{2}}βˆ’\mathrm{1}>\right) \\ $$$$=_{{t}βˆ’\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}}=\sqrt{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}{u}} \:\:\:\:\:\:\:\:\:\int_{\frac{\mathrm{2}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}\sqrt{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}}} ^{\frac{\mathrm{2}\sqrt{\mathrm{2}}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}\sqrt{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}}} \:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\:\:\sqrt{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}{du} \\ $$$$=\sqrt{\frac{\mathrm{2}}{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}}\:\left\{\:{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}\sqrt{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}}\right)βˆ’{arctan}\left(\frac{\mathrm{2}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}}{\mathrm{2}\sqrt{\frac{\lambda^{\mathrm{2}} βˆ’\mathrm{1}}{\mathrm{2}}}}\right)\right\} \\ $$$$=\sqrt{\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}βˆ’\mathrm{1}}}\left\{\:{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}}{\mathrm{2}\sqrt{\frac{\sqrt{\mathrm{2}}βˆ’\mathrm{1}}{\mathrm{2}}}}\right)βˆ’{arctan}\left(\frac{\mathrm{2}βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}}{\mathrm{2}\sqrt{\frac{\sqrt{\mathrm{2}}βˆ’\mathrm{1}}{\mathrm{2}}}}\right)\right\}{alsl} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{t}\:+\lambda^{\mathrm{2}} }\:=_{{t}\:=βˆ’{x}} \:\:\:\:\:\int_{βˆ’\mathrm{1}} ^{βˆ’\sqrt{\mathrm{2}}} \:\:\:\:\:\frac{βˆ’{dx}}{{x}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{x}\:+\lambda^{\mathrm{2}} }\: \\ $$$$=βˆ’\int_{βˆ’\mathrm{1}} ^{βˆ’\sqrt{\mathrm{2}}} \:\:\:\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} βˆ’\sqrt{\mathrm{2}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{x}+\lambda^{\mathrm{2}} }\:=….. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
you are welcome sir.
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by tanmay last updated on 06/Jun/19
∫_0 ^(Ο€/4) (√(1+tanx)) dx 1+tanx=a^2 sec^2 xΓ—(dx/da)=2a dx=((2ada)/(1+(a^2 βˆ’1)^2 )) ∫_1 ^(√2) ((2ada)/({1+(a^2 βˆ’1)^2 }))Γ—a ∫_1 ^(√2) ((2a^2 )/(a^4 βˆ’2a^2 +2))da ∫_1 ^(√2) (2/(a^2 βˆ’2+(2/a^2 )))da ∫_1 ^(√2) ((1βˆ’((√2)/a^2 )+1+((√2)/a^2 ))/(a^2 +(2/a^2 )βˆ’2))da ∫_1 ^(√2) ((d(a+((√2)/a)))/((a+((√2)/a))^2 βˆ’2(√2) βˆ’2))+∫_1 ^(√2) ((d(aβˆ’((√2)/a)))/((aβˆ’((√2)/a))^2 +2(√2) βˆ’2)) using formula ∫(dx/(x^2 βˆ’a^2 )) and∫(dx/(x^2 +a^2 )) =∫_1 ^(√2) ((d(a+((√2)/a)))/((a+((√2)/a))^2 βˆ’{(√((2(√2) +2))) }^2 )) +∫_1 ^(√2) ((d(aβˆ’((√2)/a)))/((aβˆ’((√2)/a))^2 +{(√(2(√2) βˆ’2)) }^2 )) =(1/(2{(√(2(√(2 )) +2)) }))Γ—βˆ£ln(((a+((√2)/a)βˆ’(√((2(√2) +2)) })/(a+((√2)/a)+(√(2(√2) +2)))))+(1/({(√(2(√2) βˆ’2)) }))tan^(βˆ’1) (((aβˆ’((√2)/a))/( (√(2(√2) βˆ’2)))))∣_1 ^(√2) =[(1/(2{(√(2(√2) +2)) }))Γ—{ln((((√2) +1βˆ’(√((2(√2) +2)))/( (√2) +1+(√((2(√2) +2))))}+(1/( (√(2(√2) βˆ’2))))tan^(βˆ’1) ((((√2) βˆ’1)/( (√(2(√2) βˆ’2)))))]βˆ’ (1/(2{(√(2(√2) +2)) }))Γ—{ln(((1+(√2) βˆ’(√(2(√2) +2)))/(1+(√2) +(√(2(√2) +2))))}βˆ’(1/( (√(2(√2) βˆ’2))))tan^(βˆ’1) (((1βˆ’(√2))/( (√(2(√2) βˆ’2))))) pls check
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+{tanx}}\:{dx} \\ $$$$\mathrm{1}+{tanx}={a}^{\mathrm{2}} \\ $$$${sec}^{\mathrm{2}} {x}Γ—\frac{{dx}}{{da}}=\mathrm{2}{a} \\ $$$${dx}=\frac{\mathrm{2}{ada}}{\mathrm{1}+\left({a}^{\mathrm{2}} βˆ’\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{\mathrm{2}{ada}}{\left\{\mathrm{1}+\left({a}^{\mathrm{2}} βˆ’\mathrm{1}\right)^{\mathrm{2}} \right\}}Γ—{a} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{2}{a}^{\mathrm{2}} }{{a}^{\mathrm{4}} βˆ’\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}}{da} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{2}}{{a}^{\mathrm{2}} βˆ’\mathrm{2}+\frac{\mathrm{2}}{{a}^{\mathrm{2}} }}{da} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}βˆ’\frac{\sqrt{\mathrm{2}}}{{a}^{\mathrm{2}} }+\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} +\frac{\mathrm{2}}{{a}^{\mathrm{2}} }βˆ’\mathrm{2}}{da} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{{d}\left({a}+\frac{\sqrt{\mathrm{2}}}{{a}}\right)}{\left({a}+\frac{\sqrt{\mathrm{2}}}{{a}}\right)^{\mathrm{2}} βˆ’\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{{d}\left({a}βˆ’\frac{\sqrt{\mathrm{2}}}{{a}}\right)}{\left({a}βˆ’\frac{\sqrt{\mathrm{2}}}{{a}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}} \\ $$$${using}\:{formula}\:\int\frac{{dx}}{{x}^{\mathrm{2}} βˆ’{a}^{\mathrm{2}} }\:\:{and}\int\frac{{dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{{d}\left({a}+\frac{\sqrt{\mathrm{2}}}{{a}}\right)}{\left({a}+\frac{\sqrt{\mathrm{2}}}{{a}}\right)^{\mathrm{2}} βˆ’\left\{\sqrt{\left(\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}\right)}\:\right\}^{\mathrm{2}} }\:+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{{d}\left({a}βˆ’\frac{\sqrt{\mathrm{2}}}{{a}}\right)}{\left({a}βˆ’\frac{\sqrt{\mathrm{2}}}{{a}}\right)^{\mathrm{2}} +\left\{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}\:\right\}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left\{\sqrt{\mathrm{2}\sqrt{\mathrm{2}\:}\:+\mathrm{2}}\:\right\}}Γ—\mid{ln}\left(\frac{\left.{a}+\frac{\sqrt{\mathrm{2}}}{{a}}βˆ’\sqrt{\left(\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}\right.}\:\right\}}{{a}+\frac{\sqrt{\mathrm{2}}}{{a}}+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}}\right)+\frac{\mathrm{1}}{\left\{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}\:\right\}}{tan}^{βˆ’\mathrm{1}} \left(\frac{{a}βˆ’\frac{\sqrt{\mathrm{2}}}{{a}}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}}\right)\mid_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}\left\{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}\:\right\}}Γ—\left\{{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}βˆ’\sqrt{\left(\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}\right.}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}+\sqrt{\left(\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}\right.}}\right\}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}}{tan}^{βˆ’\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}\:βˆ’\mathrm{1}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}}\right)\right]βˆ’\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left\{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}\:\right\}}Γ—\left\{{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:βˆ’\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}}\right\}βˆ’\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}}{tan}^{βˆ’\mathrm{1}} \left(\frac{\mathrm{1}βˆ’\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2}}}\right)\right. \\ $$$${pls}\:{check} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *