Question Number 161005 by vvvv last updated on 10/Dec/21
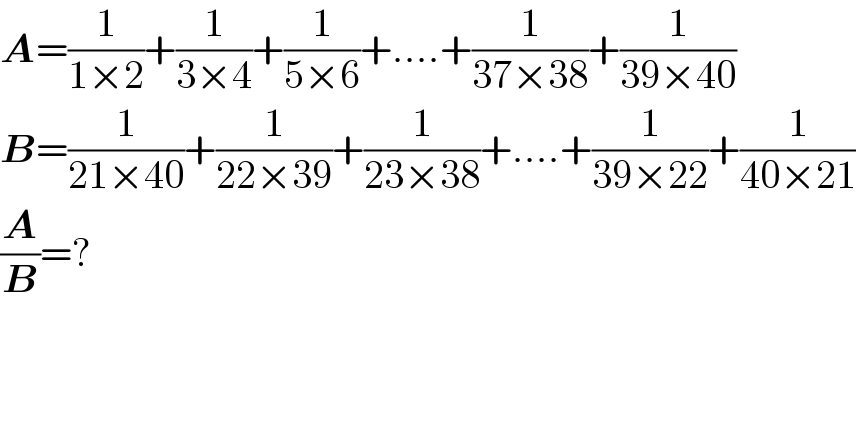
$$\boldsymbol{{A}}=\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}×\mathrm{6}}+….+\frac{\mathrm{1}}{\mathrm{37}×\mathrm{38}}+\frac{\mathrm{1}}{\mathrm{39}×\mathrm{40}} \\ $$$$\boldsymbol{{B}}=\frac{\mathrm{1}}{\mathrm{21}×\mathrm{40}}+\frac{\mathrm{1}}{\mathrm{22}×\mathrm{39}}+\frac{\mathrm{1}}{\mathrm{23}×\mathrm{38}}+….+\frac{\mathrm{1}}{\mathrm{39}×\mathrm{22}}+\frac{\mathrm{1}}{\mathrm{40}×\mathrm{21}} \\ $$$$\frac{\boldsymbol{{A}}}{\boldsymbol{{B}}}=? \\ $$
Answered by Raxreedoroid last updated on 11/Dec/21
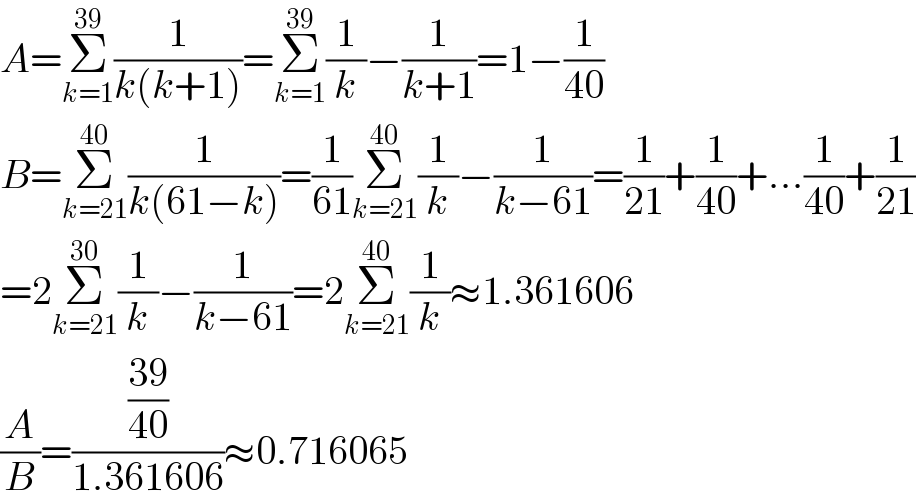
$${A}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{39}} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{39}} {\sum}}\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{40}} \\ $$$${B}=\underset{{k}=\mathrm{21}} {\overset{\mathrm{40}} {\sum}}\frac{\mathrm{1}}{{k}\left(\mathrm{61}−{k}\right)}=\frac{\mathrm{1}}{\mathrm{61}}\underset{{k}=\mathrm{21}} {\overset{\mathrm{40}} {\sum}}\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}−\mathrm{61}}=\frac{\mathrm{1}}{\mathrm{21}}+\frac{\mathrm{1}}{\mathrm{40}}+…\frac{\mathrm{1}}{\mathrm{40}}+\frac{\mathrm{1}}{\mathrm{21}} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{21}} {\overset{\mathrm{30}} {\sum}}\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}−\mathrm{61}}=\mathrm{2}\underset{{k}=\mathrm{21}} {\overset{\mathrm{40}} {\sum}}\frac{\mathrm{1}}{{k}}\approx\mathrm{1}.\mathrm{361606} \\ $$$$\frac{{A}}{{B}}=\frac{\frac{\mathrm{39}}{\mathrm{40}}}{\mathrm{1}.\mathrm{361606}}\approx\mathrm{0}.\mathrm{716065} \\ $$
