Question Number 157156 by Rasheed.Sindhi last updated on 20/Oct/21
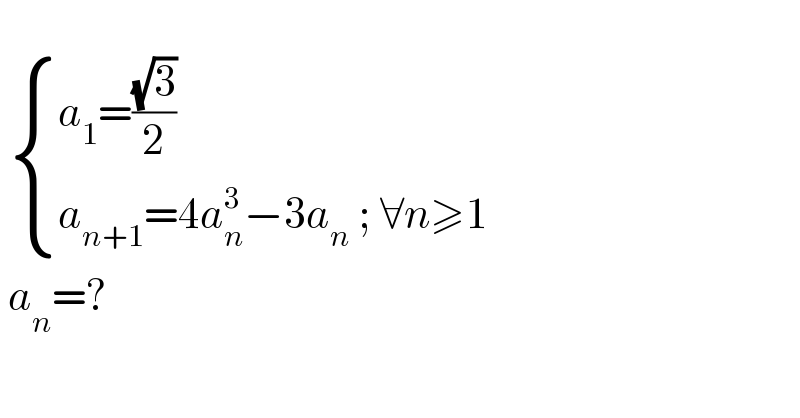
$$ \\ $$$$\:\begin{cases}{{a}_{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{{a}_{{n}+\mathrm{1}} =\mathrm{4}{a}_{{n}} ^{\mathrm{3}} −\mathrm{3}{a}_{{n}} \:;\:\forall{n}\geqslant\mathrm{1}}\end{cases} \\ $$$$\:{a}_{{n}} =? \\ $$
Answered by Rasheed.Sindhi last updated on 20/Oct/21
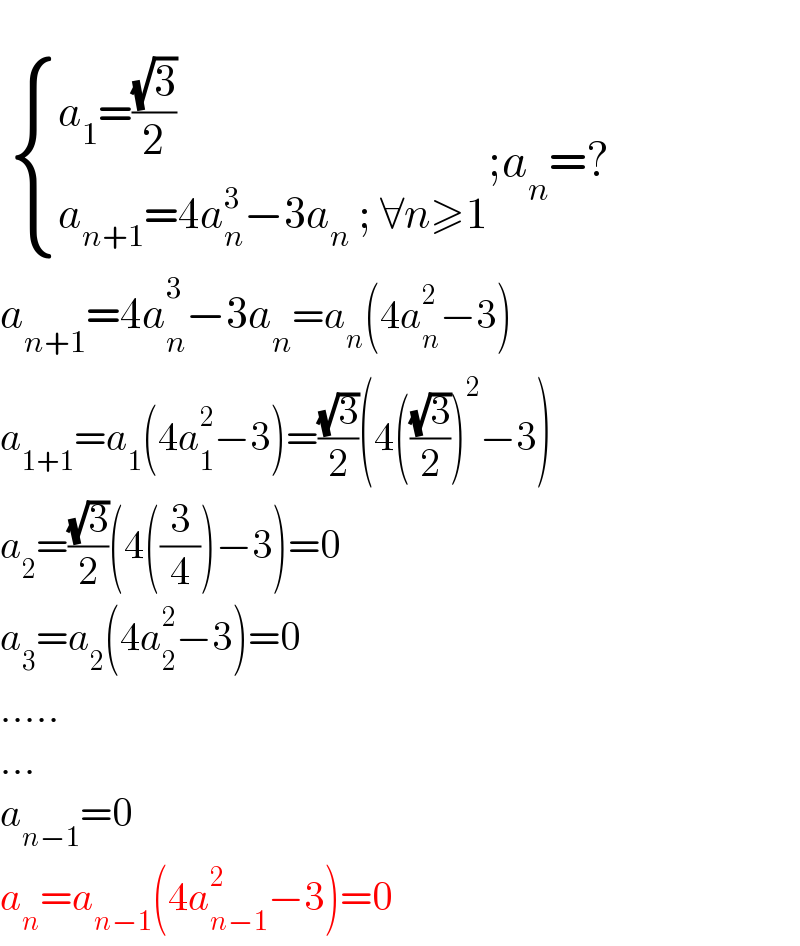
$$ \\ $$$$\:\begin{cases}{{a}_{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{{a}_{{n}+\mathrm{1}} =\mathrm{4}{a}_{{n}} ^{\mathrm{3}} −\mathrm{3}{a}_{{n}} \:;\:\forall{n}\geqslant\mathrm{1}}\end{cases};{a}_{{n}} =? \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{4}{a}_{{n}} ^{\mathrm{3}} −\mathrm{3}{a}_{{n}} ={a}_{{n}} \left(\mathrm{4}{a}_{{n}} ^{\mathrm{2}} −\mathrm{3}\right) \\ $$$${a}_{\mathrm{1}+\mathrm{1}} ={a}_{\mathrm{1}} \left(\mathrm{4}{a}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{3}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{4}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{3}\right) \\ $$$${a}_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\mathrm{3}\right)=\mathrm{0} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{2}} \left(\mathrm{4}{a}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$$….. \\ $$$$… \\ $$$${a}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} \left(\mathrm{4}{a}_{{n}−\mathrm{1}} ^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$
Commented by mr W last updated on 20/Oct/21

$${very}\:{smart}! \\ $$
Commented by cortano last updated on 20/Oct/21
$${very}\:…{very}\:{nice} \\ $$
Commented by Rasheed.Sindhi last updated on 20/Oct/21

$$\mathcal{T}{han}\mathcal{X}\:{mr}\:{W}\:\mathcal{S}{ir}! \\ $$$${Also}\:{thank}\:{you}\:{mr}\:{cortano}. \\ $$
Commented by Tawa11 last updated on 21/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Oct/21

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{miss}! \\ $$
