Menu Close

a-1-4-a-n-1-4a-n-3-a-n-2-find-a-n-

Tinku Tara 0 Comments
Pin




Question Number 81871 by mr W last updated on 16/Feb/20
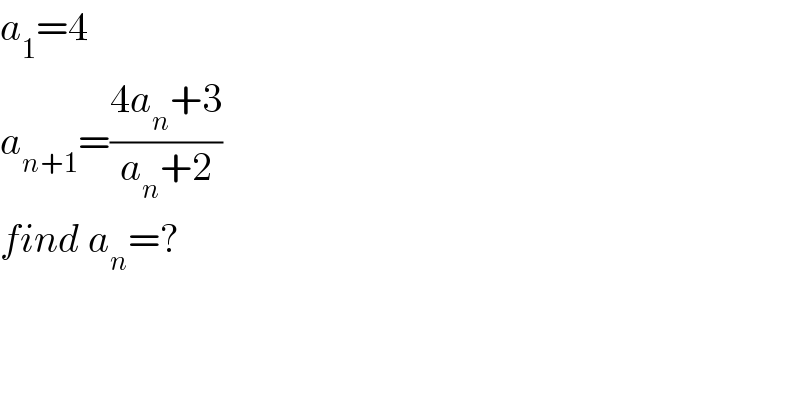
a_1 =4 a_(n+1) =((4a_n +3)/(a_n +2)) find a_n =?
$${a}_{\mathrm{1}} =\mathrm{4} \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{4}{a}_{{n}} +\mathrm{3}}{{a}_{{n}} +\mathrm{2}} \\ $$$${find}\:{a}_{{n}} =? \\ $$
Commented by jagoll last updated on 16/Feb/20
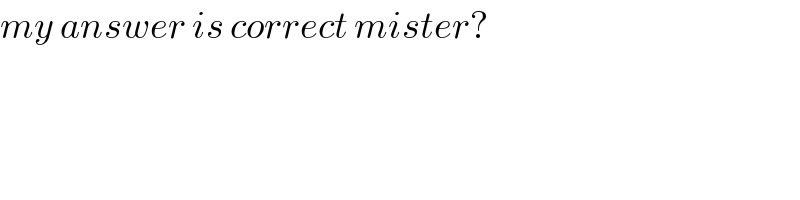
my answer is correct mister?
$${my}\:{answer}\:{is}\:{correct}\:{mister}? \\ $$
Commented by john santu last updated on 16/Feb/20
not correct! a_(n+1) = 4−(5/(a_n +2)) n=1 ⇒a_2 = 4 −(5/6)=((19)/6) n=2 ⇒a_3 = 4−(5/((((19)/6))+2))=4−((30)/(31)) = ((124−30)/(31))= ((94)/(31)) ≠ ((43)/(72))(27)−((53)/(24))
$${not}\:{correct}!\: \\ $$$${a}_{{n}+\mathrm{1}} \:=\:\mathrm{4}−\frac{\mathrm{5}}{{a}_{{n}} +\mathrm{2}} \\ $$$${n}=\mathrm{1}\:\Rightarrow{a}_{\mathrm{2}} \:=\:\mathrm{4}\:−\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{19}}{\mathrm{6}} \\ $$$${n}=\mathrm{2}\:\Rightarrow{a}_{\mathrm{3}} \:=\:\mathrm{4}−\frac{\mathrm{5}}{\left(\frac{\mathrm{19}}{\mathrm{6}}\right)+\mathrm{2}}=\mathrm{4}−\frac{\mathrm{30}}{\mathrm{31}} \\ $$$$=\:\frac{\mathrm{124}−\mathrm{30}}{\mathrm{31}}=\:\frac{\mathrm{94}}{\mathrm{31}}\:\neq\:\frac{\mathrm{43}}{\mathrm{72}}\left(\mathrm{27}\right)−\frac{\mathrm{53}}{\mathrm{24}} \\ $$
Commented by jagoll last updated on 16/Feb/20
haha...wrong sir
$${haha}…{wrong}\:{sir} \\ $$
Answered by mr W last updated on 16/Feb/20
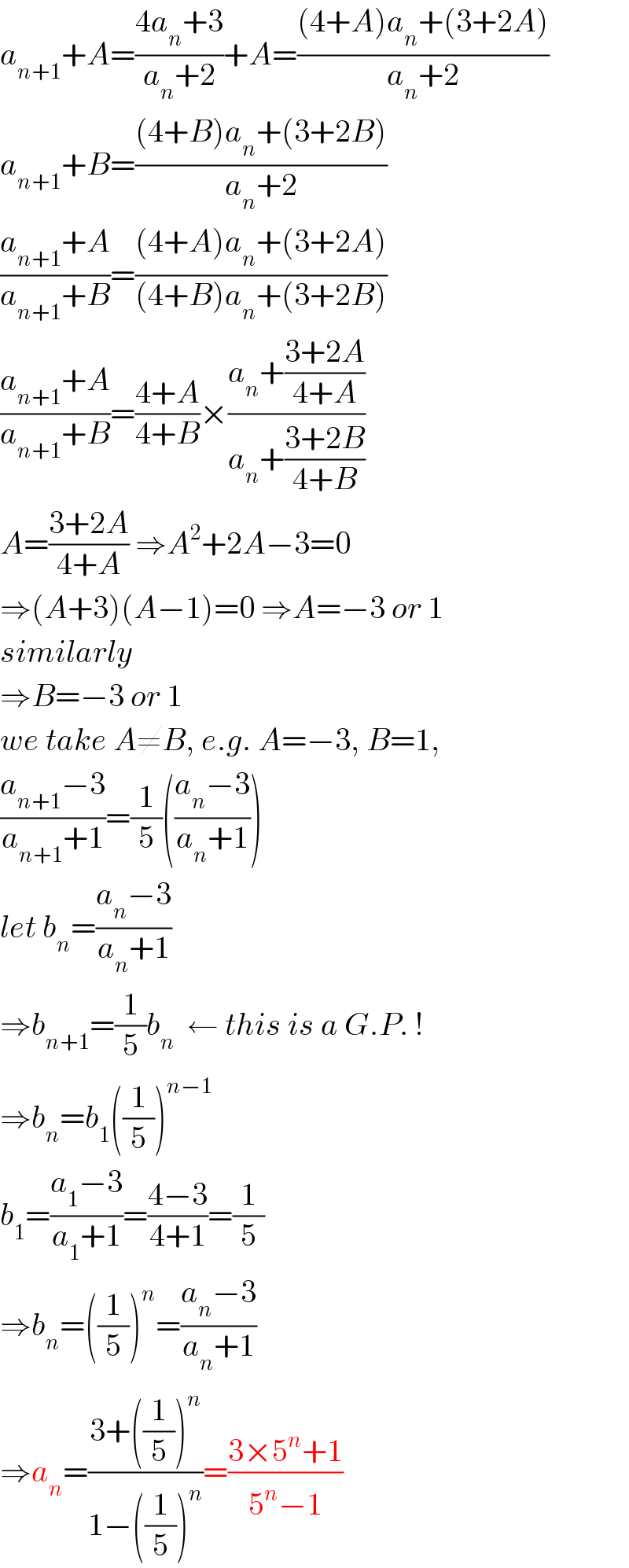
a_(n+1) +A=((4a_n +3)/(a_n +2))+A=(((4+A)a_n +(3+2A))/(a_n +2)) a_(n+1) +B=(((4+B)a_n +(3+2B))/(a_n +2)) ((a_(n+1) +A)/(a_(n+1) +B))=(((4+A)a_n +(3+2A))/((4+B)a_n +(3+2B))) ((a_(n+1) +A)/(a_(n+1) +B))=((4+A)/(4+B))×((a_n +((3+2A)/(4+A)))/(a_n +((3+2B)/(4+B)))) A=((3+2A)/(4+A)) ⇒A^2 +2A−3=0 ⇒(A+3)(A−1)=0 ⇒A=−3 or 1 similarly ⇒B=−3 or 1 we take A≠B, e.g. A=−3, B=1, ((a_(n+1) −3)/(a_(n+1) +1))=(1/5)(((a_n −3)/(a_n +1))) let b_n =((a_n −3)/(a_n +1)) ⇒b_(n+1) =(1/5)b_n ← this is a G.P. ! ⇒b_n =b_1 ((1/5))^(n−1) b_1 =((a_1 −3)/(a_1 +1))=((4−3)/(4+1))=(1/5) ⇒b_n =((1/5))^n =((a_n −3)/(a_n +1)) ⇒a_n =((3+((1/5))^n )/(1−((1/5))^n ))=((3×5^n +1)/(5^n −1))
$${a}_{{n}+\mathrm{1}} +{A}=\frac{\mathrm{4}{a}_{{n}} +\mathrm{3}}{{a}_{{n}} +\mathrm{2}}+{A}=\frac{\left(\mathrm{4}+{A}\right){a}_{{n}} +\left(\mathrm{3}+\mathrm{2}{A}\right)}{{a}_{{n}} +\mathrm{2}} \\ $$$${a}_{{n}+\mathrm{1}} +{B}=\frac{\left(\mathrm{4}+{B}\right){a}_{{n}} +\left(\mathrm{3}+\mathrm{2}{B}\right)}{{a}_{{n}} +\mathrm{2}} \\ $$$$\frac{{a}_{{n}+\mathrm{1}} +{A}}{{a}_{{n}+\mathrm{1}} +{B}}=\frac{\left(\mathrm{4}+{A}\right){a}_{{n}} +\left(\mathrm{3}+\mathrm{2}{A}\right)}{\left(\mathrm{4}+{B}\right){a}_{{n}} +\left(\mathrm{3}+\mathrm{2}{B}\right)} \\ $$$$\frac{{a}_{{n}+\mathrm{1}} +{A}}{{a}_{{n}+\mathrm{1}} +{B}}=\frac{\mathrm{4}+{A}}{\mathrm{4}+{B}}×\frac{{a}_{{n}} +\frac{\mathrm{3}+\mathrm{2}{A}}{\mathrm{4}+{A}}}{{a}_{{n}} +\frac{\mathrm{3}+\mathrm{2}{B}}{\mathrm{4}+{B}}} \\ $$$${A}=\frac{\mathrm{3}+\mathrm{2}{A}}{\mathrm{4}+{A}}\:\Rightarrow{A}^{\mathrm{2}} +\mathrm{2}{A}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left({A}+\mathrm{3}\right)\left({A}−\mathrm{1}\right)=\mathrm{0}\:\Rightarrow{A}=−\mathrm{3}\:{or}\:\mathrm{1} \\ $$$${similarly} \\ $$$$\Rightarrow{B}=−\mathrm{3}\:{or}\:\mathrm{1} \\ $$$${we}\:{take}\:{A}\neq{B},\:{e}.{g}.\:{A}=−\mathrm{3},\:{B}=\mathrm{1}, \\ $$$$\frac{{a}_{{n}+\mathrm{1}} −\mathrm{3}}{{a}_{{n}+\mathrm{1}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{5}}\left(\frac{{a}_{{n}} −\mathrm{3}}{{a}_{{n}} +\mathrm{1}}\right) \\ $$$${let}\:{b}_{{n}} =\frac{{a}_{{n}} −\mathrm{3}}{{a}_{{n}} +\mathrm{1}} \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{5}}{b}_{{n}} \:\:\leftarrow\:{this}\:{is}\:{a}\:{G}.{P}.\:! \\ $$$$\Rightarrow{b}_{{n}} ={b}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}−\mathrm{1}} \\ $$$${b}_{\mathrm{1}} =\frac{{a}_{\mathrm{1}} −\mathrm{3}}{{a}_{\mathrm{1}} +\mathrm{1}}=\frac{\mathrm{4}−\mathrm{3}}{\mathrm{4}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow{b}_{{n}} =\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}} =\frac{{a}_{{n}} −\mathrm{3}}{{a}_{{n}} +\mathrm{1}} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{3}+\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}} }{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}} }=\frac{\mathrm{3}×\mathrm{5}^{{n}} +\mathrm{1}}{\mathrm{5}^{{n}} −\mathrm{1}} \\ $$
Commented by jagoll last updated on 16/Feb/20
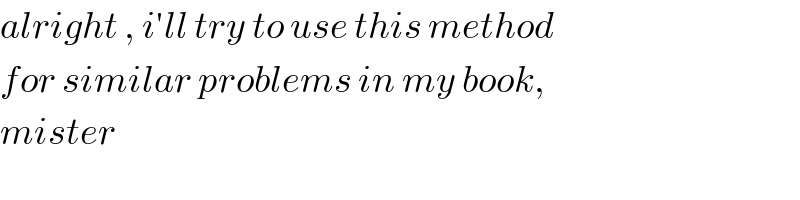
alright , i′ll try to use this method for similar problems in my book, mister
$${alright}\:,\:{i}'{ll}\:{try}\:{to}\:{use}\:{this}\:{method} \\ $$$${for}\:{similar}\:{problems}\:{in}\:{my}\:{book}, \\ $$$${mister} \\ $$
Commented by jagoll last updated on 16/Feb/20
why is it different from the previous problem? that you post too. what is the general form of solving this type of problem?
$${why}\:{is}\:{it}\:{different}\:{from}\:{the} \\ $$$${previous}\:{problem}?\:{that}\:{you}\:{post} \\ $$$${too}.\:{what}\:{is}\:{the}\:{general}\: \\ $$$${form}\:{of}\:{solving}\:{this}\:{type}\:{of} \\ $$$${problem}? \\ $$
Commented by mr W last updated on 16/Feb/20
for type a_(n+1) =2a_n −3a_(n−1) you can see that the term should be in form a_n =Aq^n , since it fulfulls the eqn. a_(n+1) =2a_n −3a_(n−1) . but you can not apply it for other types like a_(n+1) =(n+1)a_n −2a_(n−1) . that means there are no universal methods! one should try different methods from case to case. for same types you can find no solution, e.g. a_(n+1) =2a_n ^2 +1, a_(n+1) =(√(a_n +2))+1 etc.
$${for}\:{type}\:{a}_{{n}+\mathrm{1}} =\mathrm{2}{a}_{{n}} −\mathrm{3}{a}_{{n}−\mathrm{1}} \:\:{you}\:{can} \\ $$$${see}\:{that}\:{the}\:{term}\:{should}\:{be}\:{in}\:{form} \\ $$$${a}_{{n}} ={Aq}^{{n}} ,\:{since}\:{it}\:{fulfulls}\:{the}\:{eqn}. \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{2}{a}_{{n}} −\mathrm{3}{a}_{{n}−\mathrm{1}} .\:{but}\:{you}\:{can}\:{not}\:{apply} \\ $$$${it}\:{for}\:{other}\:{types}\:{like}\:{a}_{{n}+\mathrm{1}} =\left({n}+\mathrm{1}\right){a}_{{n}} −\mathrm{2}{a}_{{n}−\mathrm{1}} . \\ $$$${that}\:{means}\:{there}\:{are}\:{no}\:{universal} \\ $$$${methods}!\:{one}\:{should}\:{try}\:{different} \\ $$$${methods}\:{from}\:{case}\:{to}\:{case}.\:{for} \\ $$$${same}\:{types}\:{you}\:{can}\:{find}\:{no}\:{solution}, \\ $$$${e}.{g}.\:{a}_{{n}+\mathrm{1}} =\mathrm{2}{a}_{{n}} ^{\mathrm{2}} +\mathrm{1},\:{a}_{{n}+\mathrm{1}} =\sqrt{{a}_{{n}} +\mathrm{2}}+\mathrm{1}\:{etc}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *