Menu Close

A-1-cos-2-x-1-sin-4-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 183706 by cortano1 last updated on 29/Dec/22
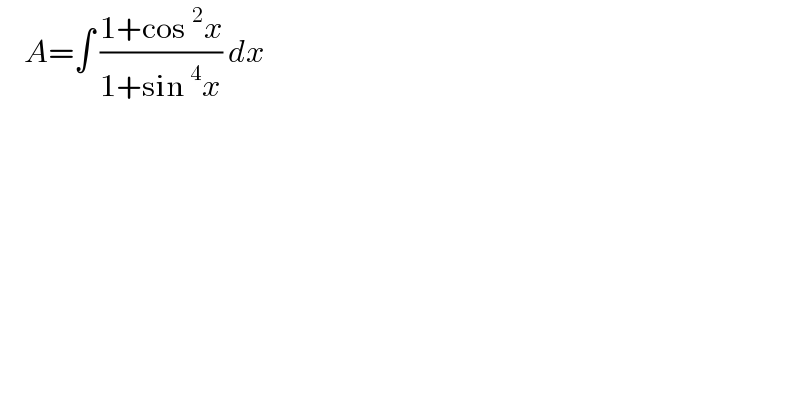
A=∫ ((1+cos^2 x)/(1+sin^4 x)) dx
$$\:\:\:\:{A}=\int\:\frac{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{sin}\:^{\mathrm{4}} {x}}\:{dx} \\ $$
Answered by Ar Brandon last updated on 29/Dec/22
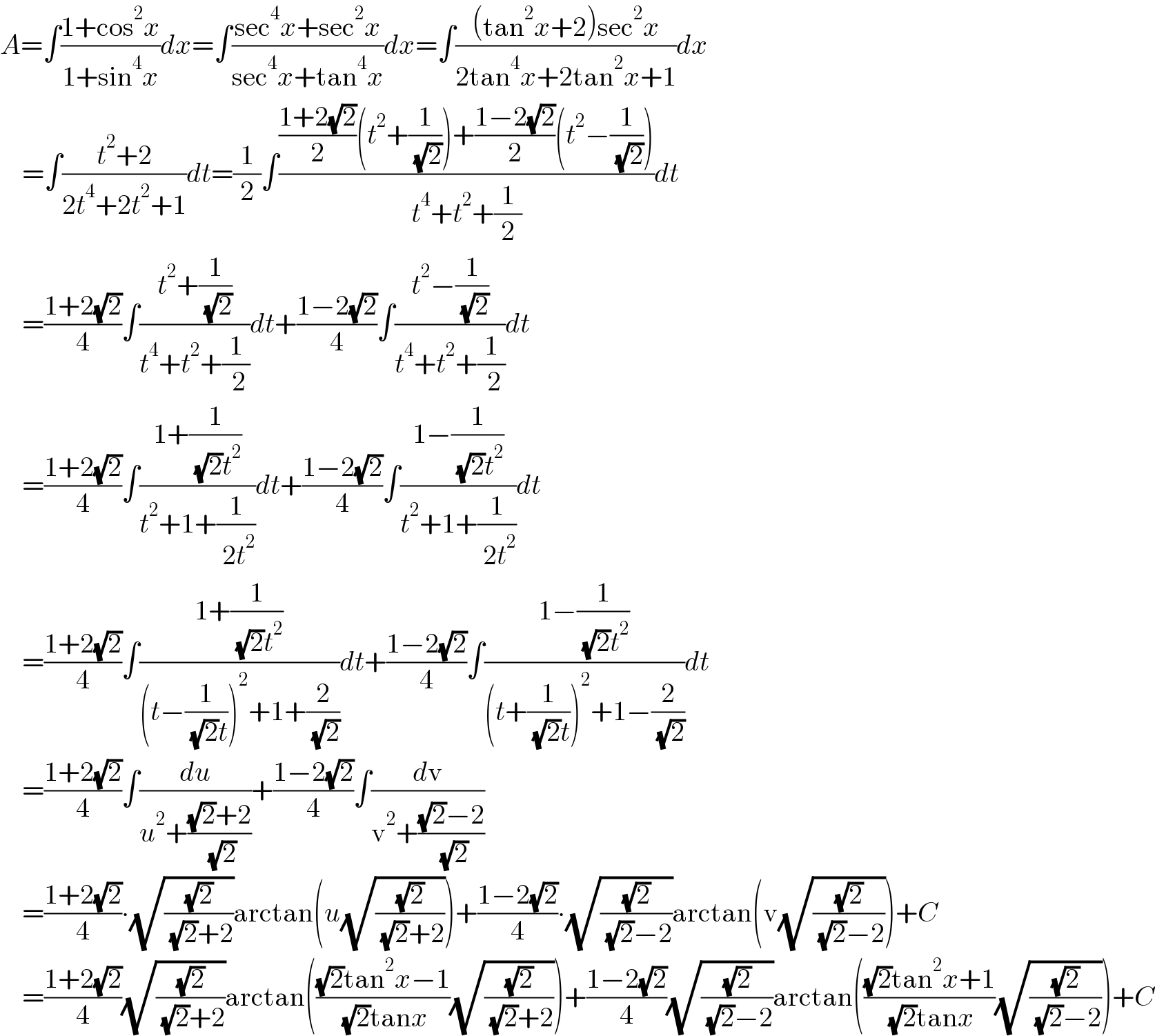
A=∫((1+cos^2 x)/(1+sin^4 x))dx=∫((sec^4 x+sec^2 x)/(sec^4 x+tan^4 x))dx=∫(((tan^2 x+2)sec^2 x)/(2tan^4 x+2tan^2 x+1))dx =∫((t^2 +2)/(2t^4 +2t^2 +1))dt=(1/2)∫((((1+2(√2))/2)(t^2 +(1/( (√2))))+((1−2(√2))/2)(t^2 −(1/( (√2)))))/(t^4 +t^2 +(1/2)))dt =((1+2(√2))/4)∫((t^2 +(1/( (√2))))/(t^4 +t^2 +(1/( 2))))dt+((1−2(√2))/4)∫((t^2 −(1/( (√2))))/(t^4 +t^2 +(1/( 2))))dt =((1+2(√2))/4)∫((1+(1/( (√2)t^2 )))/(t^2 +1+(1/( 2t^2 ))))dt+((1−2(√2))/4)∫((1−(1/( (√2)t^2 )))/(t^2 +1+(1/( 2t^2 ))))dt =((1+2(√2))/4)∫((1+(1/( (√2)t^2 )))/((t−(1/( (√2)t)))^2 +1+(2/( (√2)))))dt+((1−2(√2))/4)∫((1−(1/( (√2)t^2 )))/((t+(1/( (√2)t)))^2 +1−(2/( (√2)))))dt =((1+2(√2))/4)∫(du/(u^2 +(((√2)+2)/( (√2)))))+((1−2(√2))/4)∫(dv/(v^2 +(((√2)−2)/( (√2))))) =((1+2(√2))/4)∙(√((√2)/( (√2)+2)))arctan(u(√((√2)/( (√2)+2))))+((1−2(√2))/4)∙(√((√2)/( (√2)−2)))arctan(v(√((√2)/( (√2)−2))))+C =((1+2(√2))/4)(√((√2)/( (√2)+2)))arctan((((√2)tan^2 x−1)/( (√2)tanx))(√((√2)/( (√2)+2))))+((1−2(√2))/4)(√((√2)/( (√2)−2)))arctan((((√2)tan^2 x+1)/( (√2)tanx))(√((√2)/( (√2)−2))))+C
$${A}=\int\frac{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{sin}^{\mathrm{4}} {x}}{dx}=\int\frac{\mathrm{sec}^{\mathrm{4}} {x}+\mathrm{sec}^{\mathrm{2}} {x}}{\mathrm{sec}^{\mathrm{4}} {x}+\mathrm{tan}^{\mathrm{4}} {x}}{dx}=\int\frac{\left(\mathrm{tan}^{\mathrm{2}} {x}+\mathrm{2}\right)\mathrm{sec}^{\mathrm{2}} {x}}{\mathrm{2tan}^{\mathrm{4}} {x}+\mathrm{2tan}^{\mathrm{2}} {x}+\mathrm{1}}{dx} \\ $$$$\:\:\:\:=\int\frac{{t}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\:\mathrm{2}}}{dt}+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{t}^{\mathrm{2}} −\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\:\mathrm{2}}}{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\:\mathrm{2}{t}^{\mathrm{2}} }}{dt}+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\:\mathrm{2}{t}^{\mathrm{2}} }}{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}^{\mathrm{2}} }}{\left({t}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}}\right)^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}}{dt}+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}^{\mathrm{2}} }}{\left({t}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}}\right)^{\mathrm{2}} +\mathrm{1}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}}{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}}+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{d}\mathrm{v}}{\mathrm{v}^{\mathrm{2}} +\frac{\sqrt{\mathrm{2}}−\mathrm{2}}{\:\sqrt{\mathrm{2}}}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\centerdot\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{2}}}\mathrm{arctan}\left({u}\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{2}}}\right)+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\centerdot\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{2}}}\mathrm{arctan}\left(\mathrm{v}\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{2}}}\right)+{C} \\ $$$$\:\:\:\:=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{2}}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}\mathrm{tan}^{\mathrm{2}} {x}−\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{tan}{x}}\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{2}}}\right)+\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{2}}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}\mathrm{tan}^{\mathrm{2}} {x}+\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{tan}{x}}\sqrt{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{2}}}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *