Menu Close

a-1-e-x-1-e-x-1-2-dx-b-lnx-1-x-c-e-e-sin-lnx-dx-

Tinku Tara 0 Comments
Pin




Question Number 57819 by behi83417@gmail.com last updated on 12/Apr/19
a. ∫ [((1−e^x )/(1+e^x ))]^(1/2) dx=? b. ∫ ((lnx)/( (√(1+x))))=? c. ∫_( (√e)) ^( e) sin(lnx)dx=?
$$\boldsymbol{\mathrm{a}}.\:\:\int\:\:\:\left[\frac{\mathrm{1}−\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} }{\mathrm{1}+\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} }\right]\:^{\frac{\mathrm{1}}{\mathrm{2}}} \:\boldsymbol{\mathrm{dx}}=? \\ $$$$\boldsymbol{\mathrm{b}}.\:\:\:\:\:\int\:\:\frac{\boldsymbol{\mathrm{lnx}}}{\:\sqrt{\mathrm{1}+\boldsymbol{\mathrm{x}}}}=? \\ $$$$\boldsymbol{\mathrm{c}}.\:\:\:\:\:\:\:\underset{\:\sqrt{\boldsymbol{\mathrm{e}}}} {\overset{\:\:\:\:\:\boldsymbol{\mathrm{e}}} {\int}}\:\:\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{lnx}}\right)\boldsymbol{\mathrm{dx}}=? \\ $$
Commented by Abdo msup. last updated on 13/Apr/19
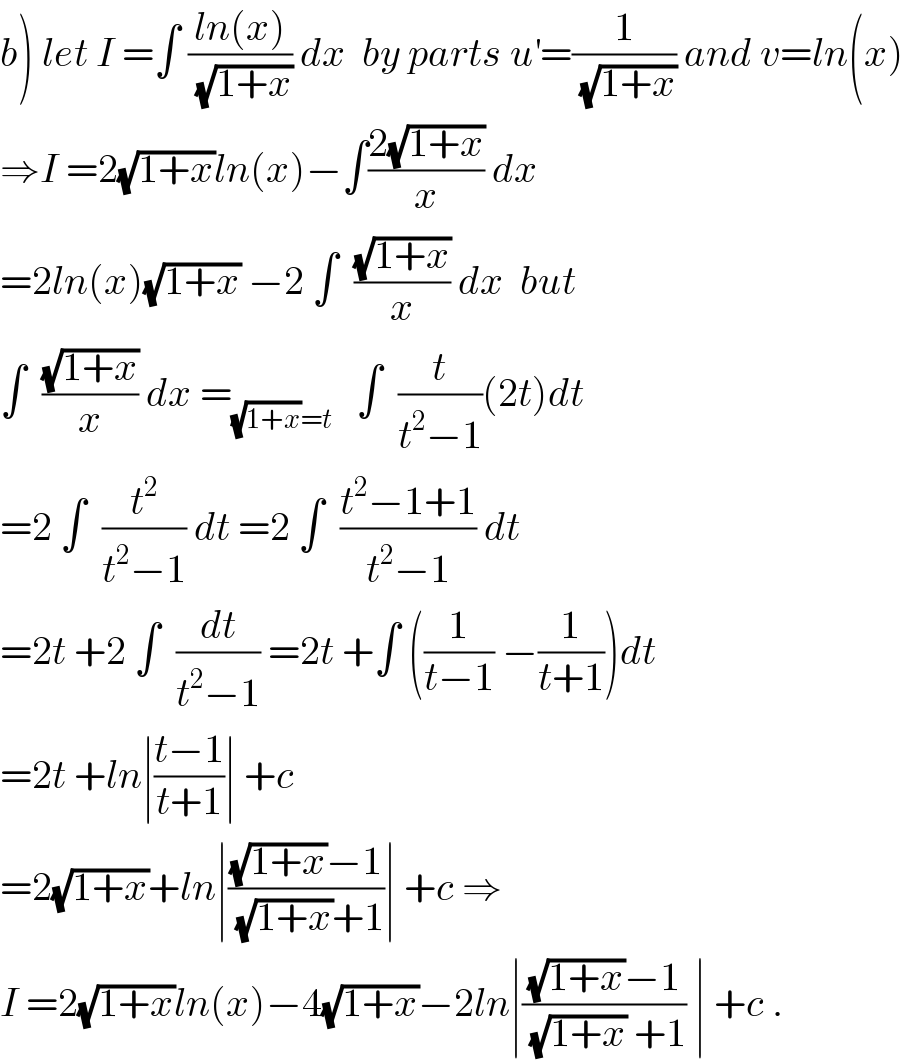
b) let I =∫ ((ln(x))/( (√(1+x)))) dx by parts u^′ =(1/( (√(1+x)))) and v=ln(x) ⇒I =2(√(1+x))ln(x)−∫((2(√(1+x)))/x) dx =2ln(x)(√(1+x)) −2 ∫ ((√(1+x))/x) dx but ∫ ((√(1+x))/x) dx =_((√(1+x))=t) ∫ (t/(t^2 −1))(2t)dt =2 ∫ (t^2 /(t^2 −1)) dt =2 ∫ ((t^2 −1+1)/(t^2 −1)) dt =2t +2 ∫ (dt/(t^2 −1)) =2t +∫ ((1/(t−1)) −(1/(t+1)))dt =2t +ln∣((t−1)/(t+1))∣ +c =2(√(1+x))+ln∣(((√(1+x))−1)/( (√(1+x))+1))∣ +c ⇒ I =2(√(1+x))ln(x)−4(√(1+x))−2ln∣(((√(1+x))−1)/( (√(1+x)) +1)) ∣ +c .
$$\left.{b}\right)\:{let}\:{I}\:=\int\:\frac{{ln}\left({x}\right)}{\:\sqrt{\mathrm{1}+{x}}}\:{dx}\:\:{by}\:{parts}\:{u}^{'} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}\:{and}\:{v}={ln}\left({x}\right) \\ $$$$\Rightarrow{I}\:=\mathrm{2}\sqrt{\mathrm{1}+{x}}{ln}\left({x}\right)−\int\frac{\mathrm{2}\sqrt{\mathrm{1}+{x}}}{{x}}\:{dx} \\ $$$$=\mathrm{2}{ln}\left({x}\right)\sqrt{\mathrm{1}+{x}}\:−\mathrm{2}\:\int\:\:\frac{\sqrt{\mathrm{1}+{x}}}{{x}}\:{dx}\:\:{but} \\ $$$$\int\:\:\frac{\sqrt{\mathrm{1}+{x}}}{{x}}\:{dx}\:=_{\sqrt{\mathrm{1}+{x}}={t}} \:\:\:\int\:\:\frac{{t}}{{t}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}\:{dt}\:=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}\:{dt} \\ $$$$=\mathrm{2}{t}\:+\mathrm{2}\:\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2}{t}\:+\int\:\left(\frac{\mathrm{1}}{{t}−\mathrm{1}}\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt} \\ $$$$=\mathrm{2}{t}\:+{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:+{c} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+{x}}+{ln}\mid\frac{\sqrt{\mathrm{1}+{x}}−\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}+\mathrm{1}}\mid\:+{c}\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\sqrt{\mathrm{1}+{x}}{ln}\left({x}\right)−\mathrm{4}\sqrt{\mathrm{1}+{x}}−\mathrm{2}{ln}\mid\frac{\sqrt{\mathrm{1}+{x}}−\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}\:+\mathrm{1}}\:\mid\:+{c}\:. \\ $$
Commented by behi83417@gmail.com last updated on 13/Apr/19
thank you very much proph. Abdo.
$${thank}\:{you}\:{very}\:{much}\:{proph}.\:{Abdo}. \\ $$
Commented by Abdo msup. last updated on 13/Apr/19
you are welcome .
$${you}\:{are}\:{welcome}\:. \\ $$
Commented by Abdo msup. last updated on 13/Apr/19
let I =∫(√((1−e^x )/(1+e^x )))dx changement e^x =t give I =∫ (√((1−t)/(1+t)))(dt/t) now we use ch.(√((1−t)/(1+t)))=u ⇒ ((1−t)/(1+t)) =u^2 ⇒1−t =u^2 +u^2 t ⇒1−u^2 =(1+u^2 )t ⇒ t =((1−u^2 )/(1+u^2 )) ⇒dt =((−2u(1+u^2 )−2u(1−u^2 ))/((1+u^2 )^2 )) =((−4u)/((1+u^2 )^2 ))du ⇒I =∫ u ((1+u^2 )/(1−u^2 )) ((−4u)/((1+u^2 )^2 )) du =−4 ∫ (u^2 /((1−u^2 )(1+u^2 ))) du =−2 ∫u^2 { (1/(1−u^2 )) −(1/(1+u^2 ))}du =2 ∫ (u^2 /(u^2 −1)) du +2∫ (u^2 /(1+u^2 ))du =2∫ ((u^2 −1+1)/(u^2 −1)) du +2 ∫((1+u^2 −1)/(1+u^2 )) du =2u +∫ (2/(u^2 −1)) du +2u −2 ∫ (du/(1+u^2 )) =4u +∫ ((1/(u−1)) −(1/(u+1)))du −2 ∫ (du/(1+u^2 )) =4u +ln∣((u−1)/(u+1))∣−2arctan(u)+c =4(√((1−t)/(1+t))) +ln∣(((√((1−t)/(1+t)))−1)/( (√((1−t)/(1+t)))+1))∣−2arctan((√((1−t)/(1+t))))+c I=4(√((1−e^x )/(1+e^x ))) +ln∣(((√((1−e^x )/(1+e^x )))−1)/( (√((1−e^x )/(1+e^x )))+1))∣−2arctan((√((1−e^x )/(1+e^x ))))+c
$${let}\:{I}\:=\int\sqrt{\frac{\mathrm{1}−{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }}{dx}\:\:{changement}\:{e}^{{x}} ={t}\:{give} \\ $$$${I}\:=\int\:\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}\frac{{dt}}{{t}}\:\:{now}\:{we}\:{use}\:{ch}.\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}={u}\:\Rightarrow \\ $$$$\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\:={u}^{\mathrm{2}} \:\Rightarrow\mathrm{1}−{t}\:={u}^{\mathrm{2}} \:+{u}^{\mathrm{2}} {t}\:\Rightarrow\mathrm{1}−{u}^{\mathrm{2}} =\left(\mathrm{1}+{u}^{\mathrm{2}} \right){t}\:\Rightarrow \\ $$$${t}\:=\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\:\Rightarrow{dt}\:=\frac{−\mathrm{2}{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)−\mathrm{2}{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{4}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }{du}\:\Rightarrow{I}\:=\int\:\:{u}\:\frac{\mathrm{1}+{u}^{\mathrm{2}} }{\mathrm{1}−{u}^{\mathrm{2}} }\:\frac{−\mathrm{4}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{du} \\ $$$$=−\mathrm{4}\:\int\:\:\frac{{u}^{\mathrm{2}} }{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:{du} \\ $$$$=−\mathrm{2}\:\int{u}^{\mathrm{2}} \left\{\:\:\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\right\}{du} \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} −\mathrm{1}}\:{du}\:\:+\mathrm{2}\int\:\:\frac{{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\mathrm{2}\int\:\frac{{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}\:{du}\:+\mathrm{2}\:\int\frac{\mathrm{1}+{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:{du} \\ $$$$=\mathrm{2}{u}\:+\int\:\:\frac{\mathrm{2}}{{u}^{\mathrm{2}} −\mathrm{1}}\:{du}\:+\mathrm{2}{u}\:−\mathrm{2}\:\int\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{4}{u}\:+\int\:\left(\frac{\mathrm{1}}{{u}−\mathrm{1}}\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du}\:−\mathrm{2}\:\int\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{4}{u}\:+{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid−\mathrm{2}{arctan}\left({u}\right)+{c} \\ $$$$=\mathrm{4}\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}\:+{ln}\mid\frac{\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}+\mathrm{1}}\mid−\mathrm{2}{arctan}\left(\sqrt{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}}\right)+{c} \\ $$$${I}=\mathrm{4}\sqrt{\frac{\mathrm{1}−{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }}\:+{ln}\mid\frac{\sqrt{\frac{\mathrm{1}−{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }}−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}−{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }}+\mathrm{1}}\mid−\mathrm{2}{arctan}\left(\sqrt{\frac{\mathrm{1}−{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }}\right)+{c} \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 13/Apr/19
thanks in advamce dear proph. Abdo.
$${thanks}\:{in}\:{advamce}\:{dear}\:{proph}.\:{Abdo}. \\ $$
Commented by peter frank last updated on 13/Apr/19
nice work
$${nice}\:{work} \\ $$
Commented by maxmathsup by imad last updated on 19/Apr/19
you are welcome
$${you}\:{are}\:{welcome} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
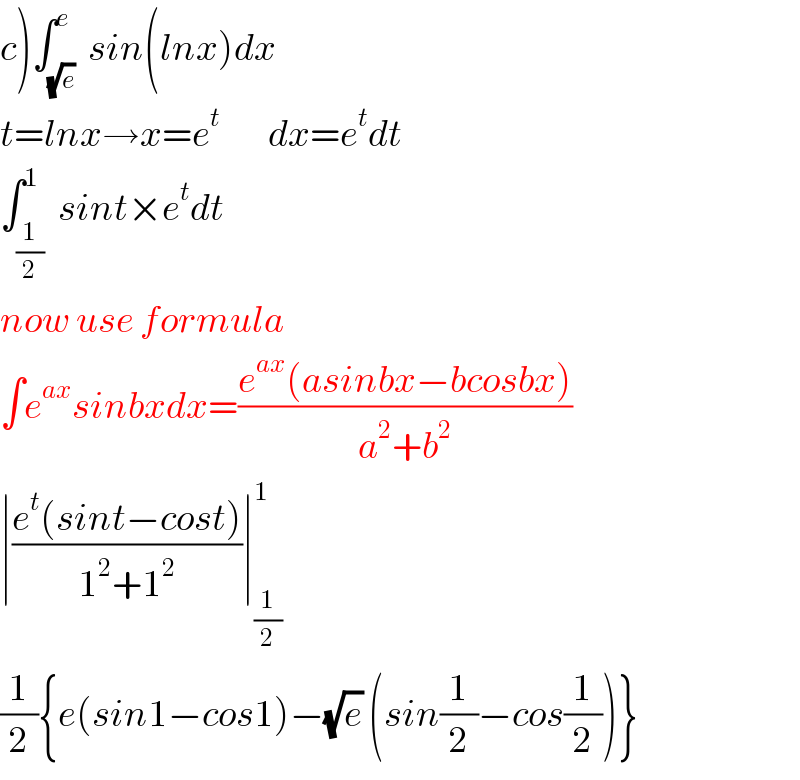
c)∫_(√e) ^e sin(lnx)dx t=lnx→x=e^t dx=e^t dt ∫_(1/2) ^1 sint×e^t dt now use formula ∫e^(ax) sinbxdx=((e^(ax) (asinbx−bcosbx))/(a^2 +b^2 )) ∣((e^t (sint−cost))/(1^2 +1^2 ))∣_(1/2) ^1 (1/2){e(sin1−cos1)−(√e) (sin(1/2)−cos(1/2))}
$$\left.{c}\right)\int_{\sqrt{{e}}} ^{{e}} \:{sin}\left({lnx}\right){dx} \\ $$$${t}={lnx}\rightarrow{x}={e}^{{t}} \:\:\:\:\:\:\:\:{dx}={e}^{{t}} {dt} \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:{sint}×{e}^{{t}} {dt} \\ $$$${now}\:{use}\:{formula}\: \\ $$$$\int{e}^{{ax}} {sinbxdx}=\frac{{e}^{{ax}} \left({asinbx}−{bcosbx}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mid\frac{{e}^{{t}} \left({sint}−{cost}\right)}{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\mid_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{{e}\left({sin}\mathrm{1}−{cos}\mathrm{1}\right)−\sqrt{{e}}\:\left({sin}\frac{\mathrm{1}}{\mathrm{2}}−{cos}\frac{\mathrm{1}}{\mathrm{2}}\right)\right\} \\ $$
Commented by behi83417@gmail.com last updated on 13/Apr/19
thank you so much sir tanmay.
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{tanmay}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
most selcome...pls check answer of a)
$$\left.{most}\:{selcome}…{pls}\:{check}\:{answer}\:{of}\:{a}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
a)∫((1−e^x )/( (√(1−e^(2x) ))))dx ∫(dx/( (√(1−e^(2x) ))))−∫((e^x dx)/( (√(1−e^(2x) )))) ∫((e^(−x) dx)/( (√(e^(−2x) −1))))−∫((e^x dx)/( (√(1−e^(2x) )))) =(−1)∫((d(e^(−x) ))/( (√((e^(−x) )^2 −1))))−∫((d(e^x ))/( (√(1−(e^x )^2 )))) now use formula ∫(dx/( (√(x^2 −a^2 ))))=ln(x+(√(x^2 −a^2 )) ) ∫(dx/( (√(a^2 −x^2 ))))=sin^(−1) ((x/a)) =(−1)ln(e^(−x) +(√(e^(−2x) −1)) )−sin^(−1) ((e^x /1))+c
$$\left.{a}\right)\int\frac{\mathrm{1}−{e}^{{x}} }{\:\sqrt{\mathrm{1}−{e}^{\mathrm{2}{x}} }}{dx} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{e}^{\mathrm{2}{x}} }}−\int\frac{{e}^{{x}} {dx}}{\:\sqrt{\mathrm{1}−{e}^{\mathrm{2}{x}} }} \\ $$$$\int\frac{{e}^{−{x}} {dx}}{\:\sqrt{{e}^{−\mathrm{2}{x}} −\mathrm{1}}}−\int\frac{{e}^{{x}} {dx}}{\:\sqrt{\mathrm{1}−{e}^{\mathrm{2}{x}} }} \\ $$$$=\left(−\mathrm{1}\right)\int\frac{{d}\left({e}^{−{x}} \right)}{\:\sqrt{\left({e}^{−{x}} \right)^{\mathrm{2}} −\mathrm{1}}}−\int\frac{{d}\left({e}^{{x}} \right)}{\:\sqrt{\mathrm{1}−\left({e}^{{x}} \right)^{\mathrm{2}} }} \\ $$$${now}\:{use}\:{formula} \\ $$$$\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}={ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:\right) \\ $$$$\int\frac{{dx}}{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}={sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right) \\ $$$$=\left(−\mathrm{1}\right){ln}\left({e}^{−{x}} +\sqrt{{e}^{−\mathrm{2}{x}} −\mathrm{1}}\:\right)−{sin}^{−\mathrm{1}} \left(\frac{{e}^{{x}} }{\mathrm{1}}\right)+{c} \\ $$
Commented by behi83417@gmail.com last updated on 13/Apr/19
your answer is right sir tanmay. thanks in advance.
$${your}\:{answer}\:{is}\:{right}\:{sir}\:{tanmay}. \\ $$$${thanks}\:{in}\:{advance}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *