Question Number 103903 by mr W last updated on 18/Jul/20

Commented by bobhans last updated on 18/Jul/20
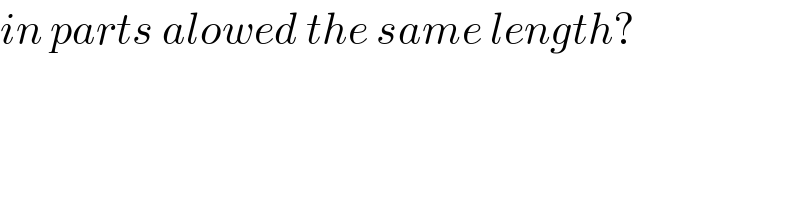
Commented by mr W last updated on 18/Jul/20

Commented by bobhans last updated on 18/Jul/20
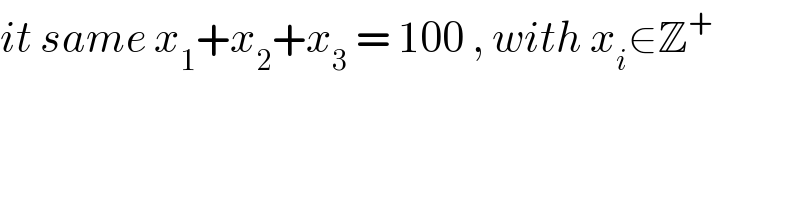
Commented by mr W last updated on 18/Jul/20

Commented by bobhans last updated on 18/Jul/20

Answered by mr W last updated on 18/Jul/20

Commented by bobhans last updated on 18/Jul/20

Commented by mr W last updated on 18/Jul/20

Commented by mr W last updated on 18/Jul/20
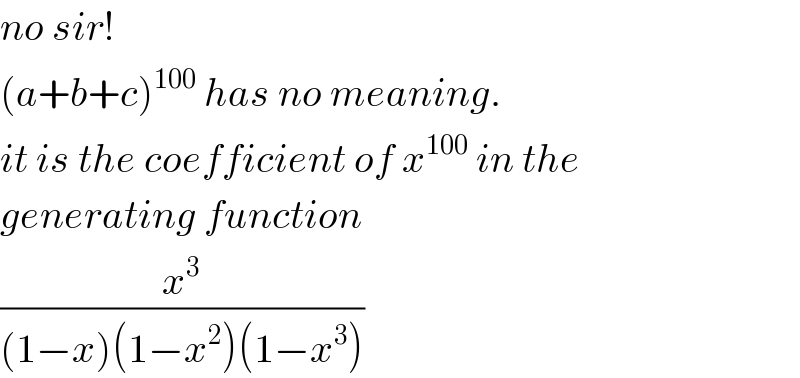
Commented by mr W last updated on 18/Jul/20

Commented by bemath last updated on 18/Jul/20
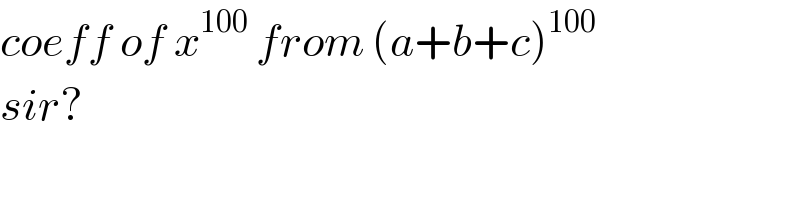
Commented by mr W last updated on 18/Jul/20
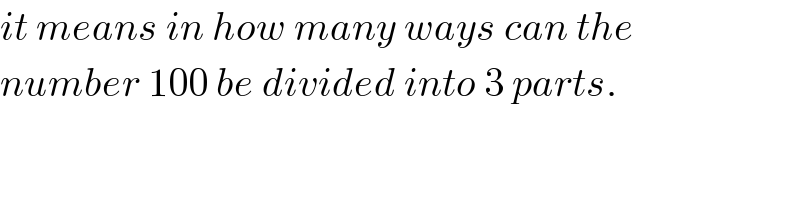
Commented by bemath last updated on 18/Jul/20
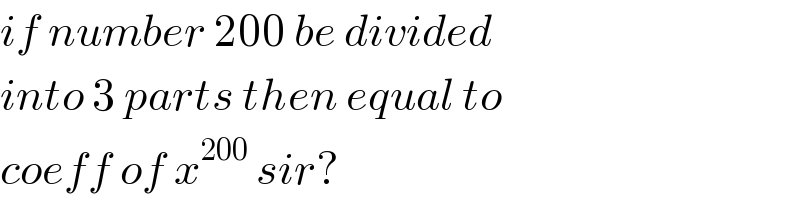
Commented by mr W last updated on 18/Jul/20

Commented by bemath last updated on 18/Jul/20

Commented by prakash jain last updated on 18/Jul/20
Some more ideas around this topic in Wikipedia
https://en.m.wikipedia.org/wiki/Partition_(number_theory)
