Question Number 55887 by behi83417@gmail.com last updated on 05/Mar/19
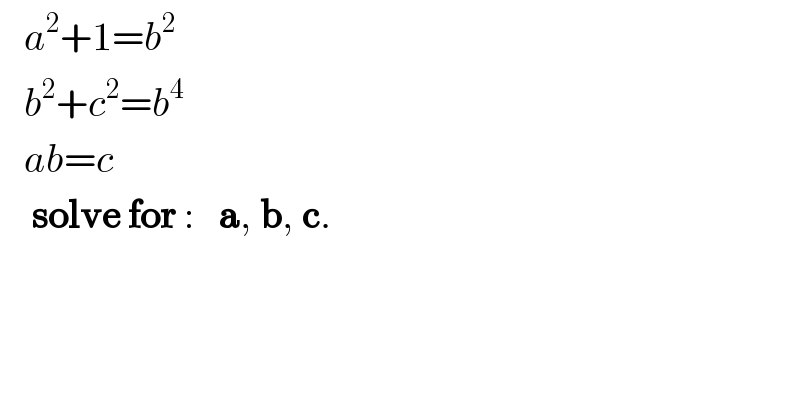
$$\:\:\:{a}^{\mathrm{2}} +\mathrm{1}={b}^{\mathrm{2}} \\ $$$$\:\:\:{b}^{\mathrm{2}} +{c}^{\mathrm{2}} ={b}^{\mathrm{4}} \\ $$$$\:\:\:{ab}={c} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\::\:\:\:\boldsymbol{\mathrm{a}},\:\boldsymbol{\mathrm{b}},\:\boldsymbol{\mathrm{c}}. \\ $$
Answered by MJS last updated on 05/Mar/19
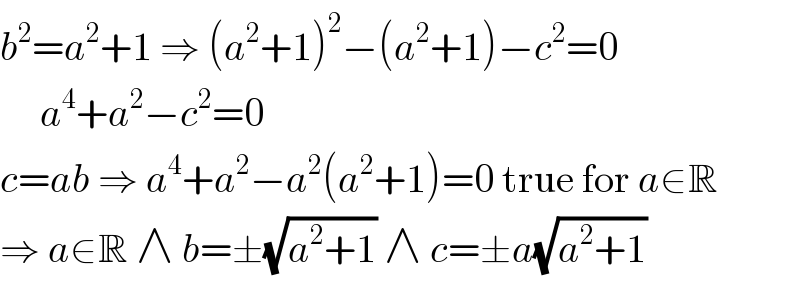
$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{1}\:\Rightarrow\:\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +\mathrm{1}\right)−{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:{a}^{\mathrm{4}} +{a}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${c}={ab}\:\Rightarrow\:{a}^{\mathrm{4}} +{a}^{\mathrm{2}} −{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0}\:\mathrm{true}\:\mathrm{for}\:{a}\in\mathbb{R} \\ $$$$\Rightarrow\:{a}\in\mathbb{R}\:\wedge\:{b}=\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\:\wedge\:{c}=\pm{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$
Answered by JDamian last updated on 06/Mar/19
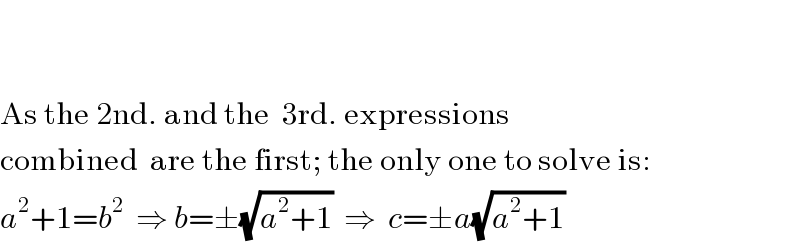
$$ \\ $$$$ \\ $$$$\mathrm{As}\:\mathrm{the}\:\mathrm{2nd}.\:\mathrm{and}\:\mathrm{the}\:\:\mathrm{3rd}.\:\mathrm{expressions} \\ $$$$\mathrm{combined}\:\:\mathrm{are}\:\mathrm{the}\:\mathrm{first};\:\mathrm{the}\:\mathrm{only}\:\mathrm{one}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{is}: \\ $$$${a}^{\mathrm{2}} +\mathrm{1}={b}^{\mathrm{2}} \:\:\Rightarrow\:{b}=\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\:\:\Rightarrow\:\:{c}=\pm{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\: \\ $$
