Question Number 185760 by mathlove last updated on 27/Jan/23
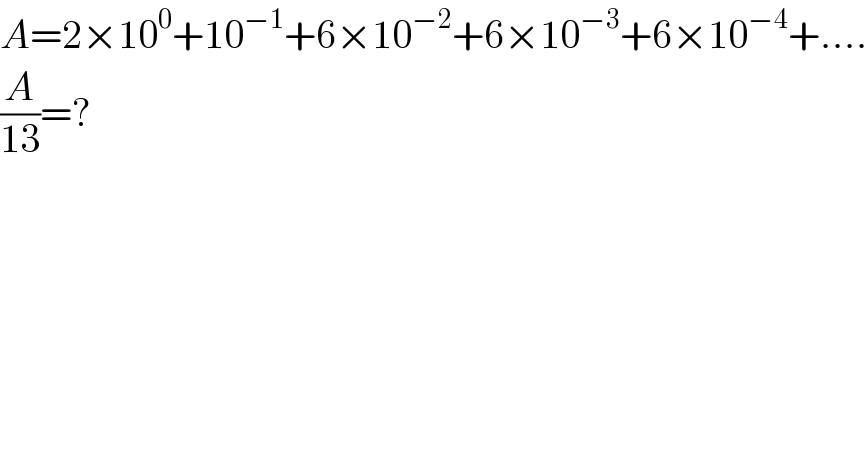
$${A}=\mathrm{2}×\mathrm{10}^{\mathrm{0}} +\mathrm{10}^{−\mathrm{1}} +\mathrm{6}×\mathrm{10}^{−\mathrm{2}} +\mathrm{6}×\mathrm{10}^{−\mathrm{3}} +\mathrm{6}×\mathrm{10}^{−\mathrm{4}} +…. \\ $$$$\frac{{A}}{\mathrm{13}}=? \\ $$
Answered by Rasheed.Sindhi last updated on 27/Jan/23
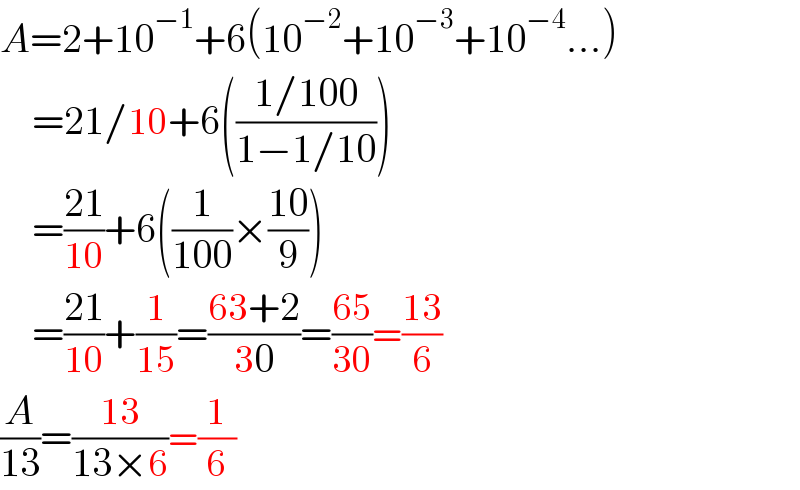
$${A}=\mathrm{2}+\mathrm{10}^{−\mathrm{1}} +\mathrm{6}\left(\mathrm{10}^{−\mathrm{2}} +\mathrm{10}^{−\mathrm{3}} +\mathrm{10}^{−\mathrm{4}} …\right) \\ $$$$\:\:\:\:=\mathrm{21}/\mathrm{10}+\mathrm{6}\left(\frac{\mathrm{1}/\mathrm{100}}{\mathrm{1}−\mathrm{1}/\mathrm{10}}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{21}}{\mathrm{10}}+\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{100}}×\frac{\mathrm{10}}{\mathrm{9}}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{21}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{15}}=\frac{\mathrm{63}+\mathrm{2}}{\mathrm{30}}=\frac{\mathrm{65}}{\mathrm{30}}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\frac{{A}}{\mathrm{13}}=\frac{\mathrm{13}}{\mathrm{13}×\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by JDamian last updated on 27/Jan/23
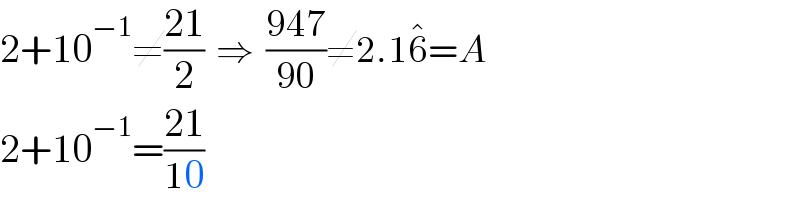
$$\mathrm{2}+\mathrm{10}^{−\mathrm{1}} \neq\frac{\mathrm{21}}{\mathrm{2}}\:\:\Rightarrow\:\:\frac{\mathrm{947}}{\mathrm{90}}\neq\mathrm{2}.\mathrm{1}\hat {\mathrm{6}}={A} \\ $$$$\mathrm{2}+\mathrm{10}^{−\mathrm{1}} =\frac{\mathrm{21}}{\mathrm{10}} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Jan/23
$$\mathcal{T}{hanks}\:{sir}!\:{My}\:{mistakes}.{I}'{ve}\:{corrected}\:{now}. \\ $$
