Question Number 24716 by Tinkutara last updated on 25/Nov/17

$$\mathrm{A}\:\mathrm{2}.\mathrm{2}\:\mathrm{kg}\:\mathrm{block}\:\mathrm{starts}\:\mathrm{from}\:\mathrm{rest}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{rough}\:\mathrm{inclined}\:\mathrm{plane}\:\mathrm{that}\:\mathrm{makes}\:\mathrm{an} \\ $$$$\mathrm{angle}\:\mathrm{of}\:\mathrm{25}°\:\mathrm{with}\:\mathrm{the}\:\mathrm{horizontal}.\:\mathrm{The} \\ $$$$\mathrm{coefficient}\:\mathrm{of}\:\mathrm{kinetic}\:\mathrm{friction}\:\mathrm{is}\:\mathrm{0}.\mathrm{25}.\:\mathrm{As} \\ $$$$\mathrm{the}\:\mathrm{block}\:\mathrm{goes}\:\mathrm{2}\:\mathrm{m}\:\mathrm{down}\:\mathrm{the}\:\mathrm{plane},\:\mathrm{the} \\ $$$$\mathrm{mechanical}\:\mathrm{energy}\:\mathrm{of}\:\mathrm{the}\:\mathrm{Earth}-\mathrm{block} \\ $$$$\mathrm{system}\:\mathrm{changes}\:\mathrm{by} \\ $$
Answered by ajfour last updated on 25/Nov/17
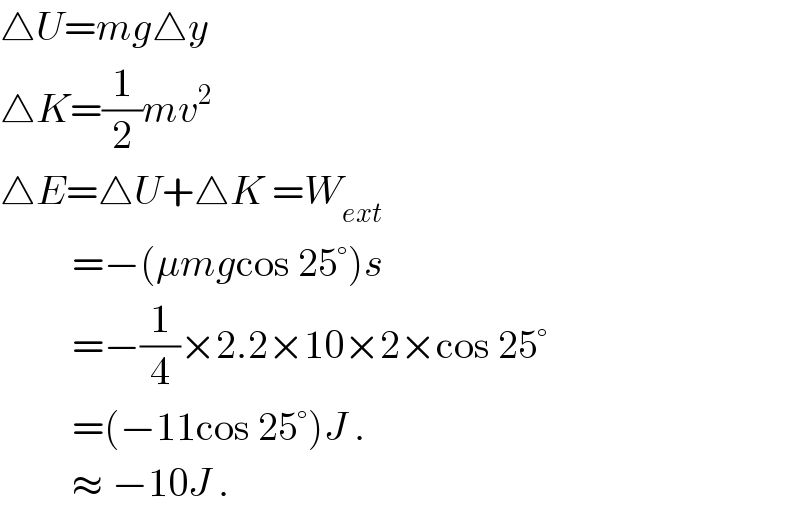
$$\bigtriangleup{U}={mg}\bigtriangleup{y} \\ $$$$\bigtriangleup{K}=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\bigtriangleup{E}=\bigtriangleup{U}+\bigtriangleup{K}\:={W}_{{ext}} \\ $$$$\:\:\:\:\:\:\:\:\:=−\left(\mu{mg}\mathrm{cos}\:\mathrm{25}°\right){s} \\ $$$$\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{2}.\mathrm{2}×\mathrm{10}×\mathrm{2}×\mathrm{cos}\:\mathrm{25}° \\ $$$$\:\:\:\:\:\:\:\:\:=\left(−\mathrm{11cos}\:\mathrm{25}°\right){J}\:. \\ $$$$\:\:\:\:\:\:\:\:\:\approx\:−\mathrm{10}{J}\:. \\ $$
Commented by Tinkutara last updated on 25/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$
