Question Number 151490 by mathdanisur last updated on 21/Aug/21
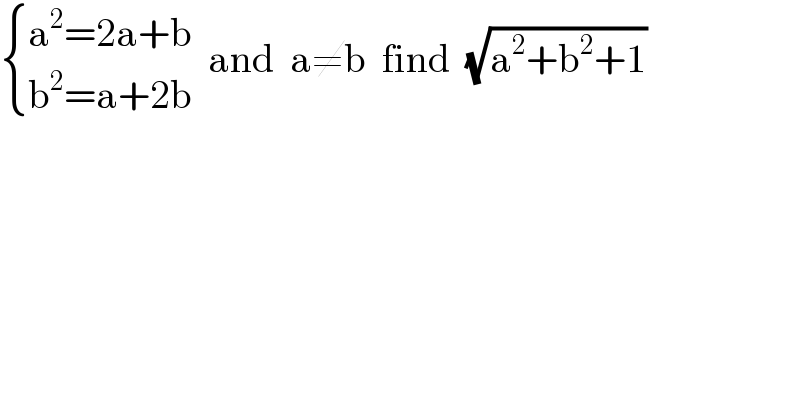
$$\begin{cases}{\mathrm{a}^{\mathrm{2}} =\mathrm{2a}+\mathrm{b}}\\{\mathrm{b}^{\mathrm{2}} =\mathrm{a}+\mathrm{2b}}\end{cases}\:\:\mathrm{and}\:\:\mathrm{a}\neq\mathrm{b}\:\:\mathrm{find}\:\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{1}} \\ $$
Answered by iloveisrael last updated on 21/Aug/21
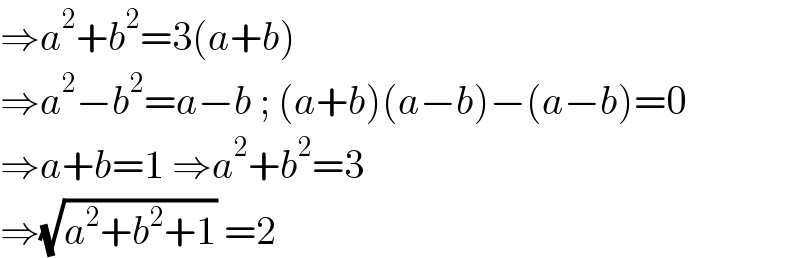
$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{3}\left({a}+{b}\right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={a}−{b}\:;\:\left({a}+{b}\right)\left({a}−{b}\right)−\left({a}−{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}+{b}=\mathrm{1}\:\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{3} \\ $$$$\Rightarrow\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{1}}\:=\mathrm{2} \\ $$
Commented by mathdanisur last updated on 21/Aug/21

$${thank}\:{you}\:{Ser} \\ $$
