Question Number 147699 by mathdanisur last updated on 22/Jul/21
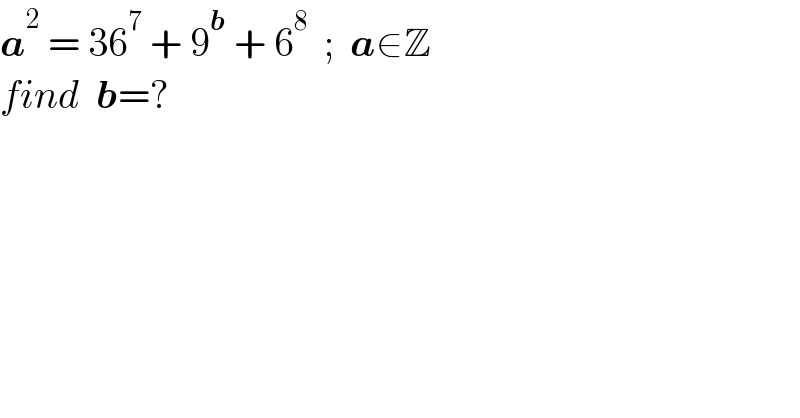
$$\boldsymbol{{a}}^{\mathrm{2}} \:=\:\mathrm{36}^{\mathrm{7}} \:+\:\mathrm{9}^{\boldsymbol{{b}}} \:+\:\mathrm{6}^{\mathrm{8}} \:\:;\:\:\boldsymbol{{a}}\in\mathbb{Z} \\ $$$${find}\:\:\boldsymbol{{b}}=? \\ $$
Answered by Olaf_Thorendsen last updated on 22/Jul/21
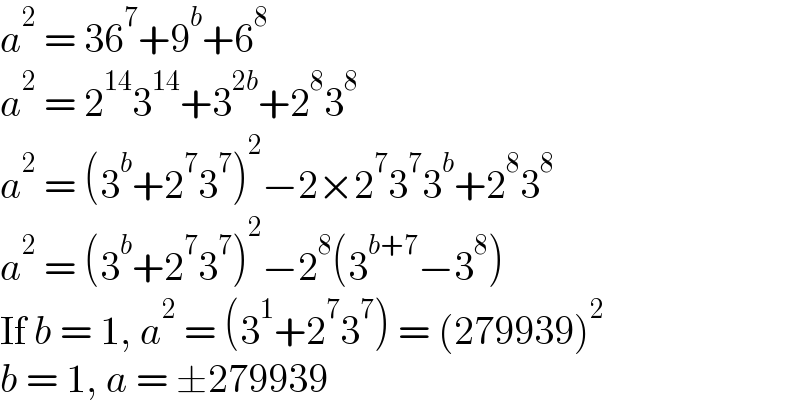
$${a}^{\mathrm{2}} \:=\:\mathrm{36}^{\mathrm{7}} +\mathrm{9}^{{b}} +\mathrm{6}^{\mathrm{8}} \\ $$$${a}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{14}} \mathrm{3}^{\mathrm{14}} +\mathrm{3}^{\mathrm{2}{b}} +\mathrm{2}^{\mathrm{8}} \mathrm{3}^{\mathrm{8}} \\ $$$${a}^{\mathrm{2}} \:=\:\left(\mathrm{3}^{{b}} +\mathrm{2}^{\mathrm{7}} \mathrm{3}^{\mathrm{7}} \right)^{\mathrm{2}} −\mathrm{2}×\mathrm{2}^{\mathrm{7}} \mathrm{3}^{\mathrm{7}} \mathrm{3}^{{b}} +\mathrm{2}^{\mathrm{8}} \mathrm{3}^{\mathrm{8}} \\ $$$${a}^{\mathrm{2}} \:=\:\left(\mathrm{3}^{{b}} +\mathrm{2}^{\mathrm{7}} \mathrm{3}^{\mathrm{7}} \right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{8}} \left(\mathrm{3}^{{b}+\mathrm{7}} −\mathrm{3}^{\mathrm{8}} \right) \\ $$$$\mathrm{If}\:{b}\:=\:\mathrm{1},\:{a}^{\mathrm{2}} \:=\:\left(\mathrm{3}^{\mathrm{1}} +\mathrm{2}^{\mathrm{7}} \mathrm{3}^{\mathrm{7}} \right)\:=\:\left(\mathrm{279939}\right)^{\mathrm{2}} \\ $$$${b}\:=\:\mathrm{1},\:{a}\:=\:\pm\mathrm{279939} \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
