Question Number 167488 by mathlove last updated on 18/Mar/22
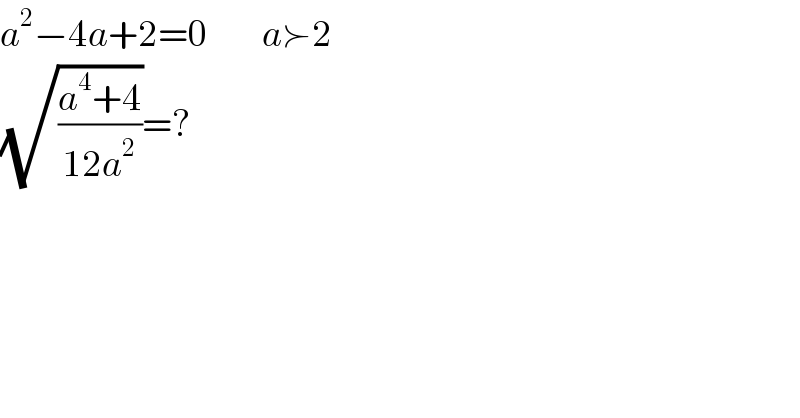
$${a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{2}=\mathrm{0}\:\:\:\:\:\:\:\:\:{a}\succ\mathrm{2} \\ $$$$\sqrt{\frac{{a}^{\mathrm{4}} +\mathrm{4}}{\mathrm{12}{a}^{\mathrm{2}} }}=? \\ $$
Commented by cortano1 last updated on 18/Mar/22
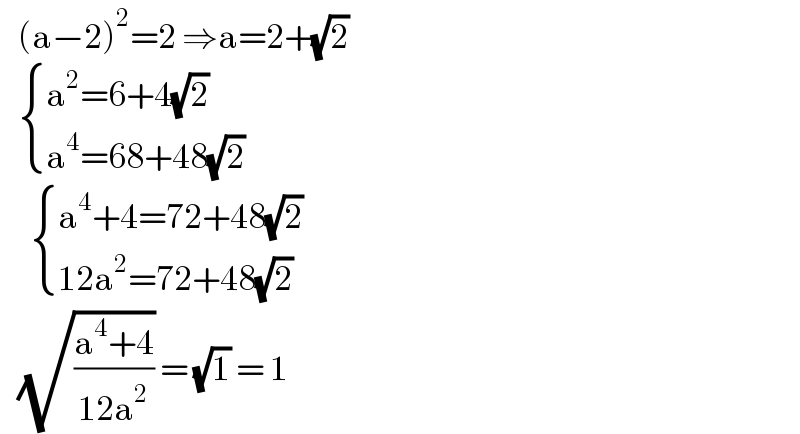
$$\:\:\:\left(\mathrm{a}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{2}\:\Rightarrow\mathrm{a}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\:\:\:\begin{cases}{\mathrm{a}^{\mathrm{2}} =\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}}\\{\mathrm{a}^{\mathrm{4}} =\mathrm{68}+\mathrm{48}\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\:\:\:\:\:\begin{cases}{\mathrm{a}^{\mathrm{4}} +\mathrm{4}=\mathrm{72}+\mathrm{48}\sqrt{\mathrm{2}}}\\{\mathrm{12a}^{\mathrm{2}} =\mathrm{72}+\mathrm{48}\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\:\:\:\sqrt{\frac{\mathrm{a}^{\mathrm{4}} +\mathrm{4}}{\mathrm{12a}^{\mathrm{2}} }}\:=\:\sqrt{\mathrm{1}}\:=\:\mathrm{1} \\ $$
Answered by mr W last updated on 18/Mar/22
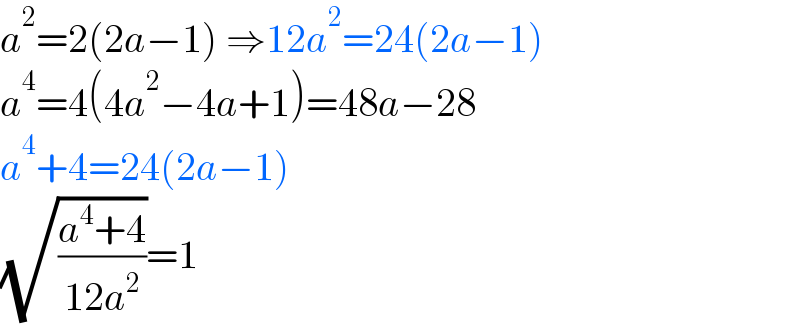
$${a}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{2}{a}−\mathrm{1}\right)\:\Rightarrow\mathrm{12}{a}^{\mathrm{2}} =\mathrm{24}\left(\mathrm{2}{a}−\mathrm{1}\right) \\ $$$${a}^{\mathrm{4}} =\mathrm{4}\left(\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{1}\right)=\mathrm{48}{a}−\mathrm{28} \\ $$$${a}^{\mathrm{4}} +\mathrm{4}=\mathrm{24}\left(\mathrm{2}{a}−\mathrm{1}\right) \\ $$$$\sqrt{\frac{{a}^{\mathrm{4}} +\mathrm{4}}{\mathrm{12}{a}^{\mathrm{2}} }}=\mathrm{1} \\ $$
