Question Number 110727 by Study last updated on 30/Aug/20
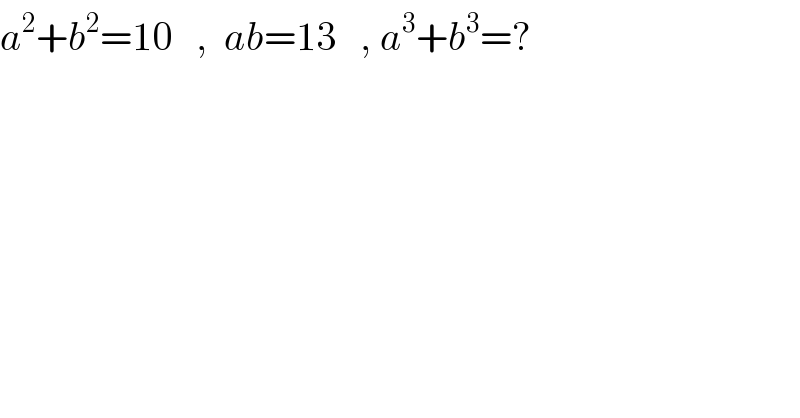
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{10}\:\:\:,\:\:{ab}=\mathrm{13}\:\:\:,\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =? \\ $$
Answered by mr W last updated on 30/Aug/20
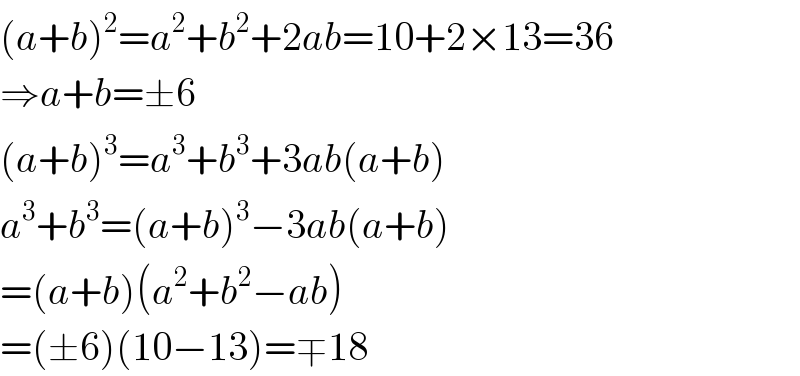
$$\left({a}+{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}=\mathrm{10}+\mathrm{2}×\mathrm{13}=\mathrm{36} \\ $$$$\Rightarrow{a}+{b}=\pm\mathrm{6} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$$=\left({a}+{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right) \\ $$$$=\left(\pm\mathrm{6}\right)\left(\mathrm{10}−\mathrm{13}\right)=\mp\mathrm{18} \\ $$
