Question Number 122405 by Khalmohmmad last updated on 16/Nov/20

$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{15} \\ $$$$\mathrm{2}{a}−{b}=? \\ $$
Commented by Dwaipayan Shikari last updated on 16/Nov/20
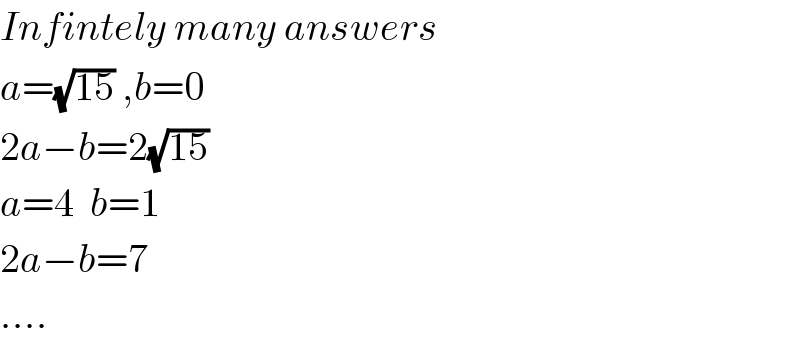
$${Infintely}\:{many}\:{answers} \\ $$$${a}=\sqrt{\mathrm{15}}\:,{b}=\mathrm{0} \\ $$$$\mathrm{2}{a}−{b}=\mathrm{2}\sqrt{\mathrm{15}} \\ $$$${a}=\mathrm{4}\:\:{b}=\mathrm{1} \\ $$$$\mathrm{2}{a}−{b}=\mathrm{7} \\ $$$$…. \\ $$
Answered by ajfour last updated on 16/Nov/20
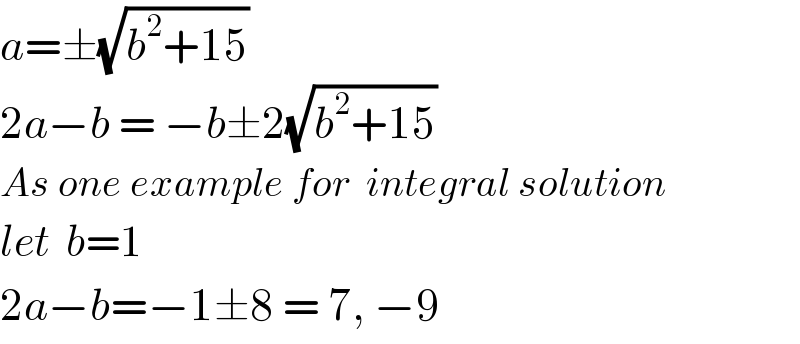
$${a}=\pm\sqrt{{b}^{\mathrm{2}} +\mathrm{15}} \\ $$$$\mathrm{2}{a}−{b}\:=\:−{b}\pm\mathrm{2}\sqrt{{b}^{\mathrm{2}} +\mathrm{15}} \\ $$$${As}\:{one}\:{example}\:{for}\:\:{integral}\:{solution} \\ $$$${let}\:\:{b}=\mathrm{1} \\ $$$$\mathrm{2}{a}−{b}=−\mathrm{1}\pm\mathrm{8}\:=\:\mathrm{7},\:−\mathrm{9} \\ $$
Answered by mr W last updated on 16/Nov/20
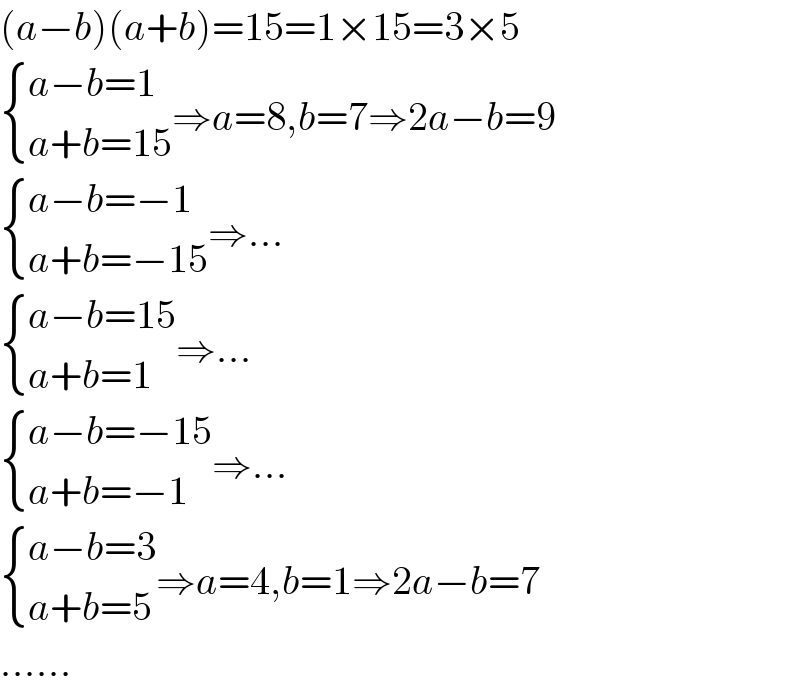
$$\left({a}−{b}\right)\left({a}+{b}\right)=\mathrm{15}=\mathrm{1}×\mathrm{15}=\mathrm{3}×\mathrm{5} \\ $$$$\begin{cases}{{a}−{b}=\mathrm{1}}\\{{a}+{b}=\mathrm{15}}\end{cases}\Rightarrow{a}=\mathrm{8},{b}=\mathrm{7}\Rightarrow\mathrm{2}{a}−{b}=\mathrm{9} \\ $$$$\begin{cases}{{a}−{b}=−\mathrm{1}}\\{{a}+{b}=−\mathrm{15}}\end{cases}\Rightarrow… \\ $$$$\begin{cases}{{a}−{b}=\mathrm{15}}\\{{a}+{b}=\mathrm{1}}\end{cases}\Rightarrow… \\ $$$$\begin{cases}{{a}−{b}=−\mathrm{15}}\\{{a}+{b}=−\mathrm{1}}\end{cases}\Rightarrow… \\ $$$$\begin{cases}{{a}−{b}=\mathrm{3}}\\{{a}+{b}=\mathrm{5}}\end{cases}\Rightarrow{a}=\mathrm{4},{b}=\mathrm{1}\Rightarrow\mathrm{2}{a}−{b}=\mathrm{7} \\ $$$$…… \\ $$
