Question Number 167650 by Rasheed.Sindhi last updated on 22/Mar/22
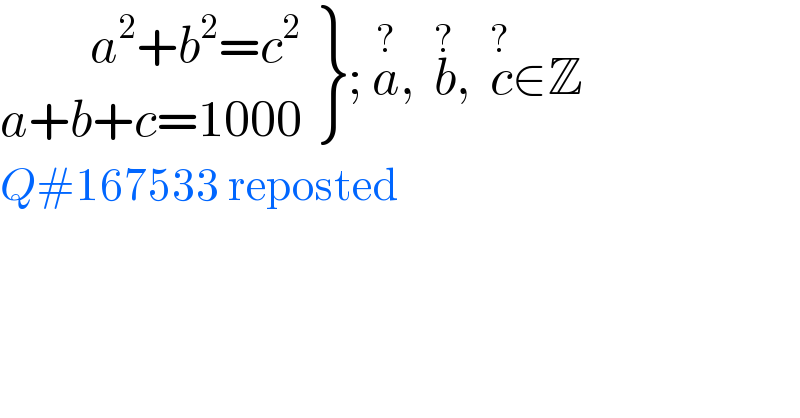
$$\left.\begin{matrix}{\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} }\\{{a}+{b}+{c}=\mathrm{1000}}\end{matrix}\right\};\:\overset{?} {{a}},\:\:\overset{?} {{b}},\:\:\overset{?} {{c}}\in\mathbb{Z} \\ $$$${Q}#\mathrm{167533}\:\mathrm{reposted} \\ $$
Commented by Ari last updated on 22/Mar/22
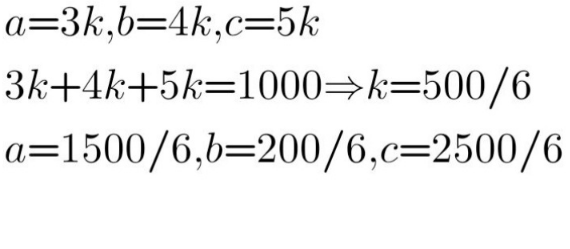
Commented by mr W last updated on 22/Mar/22
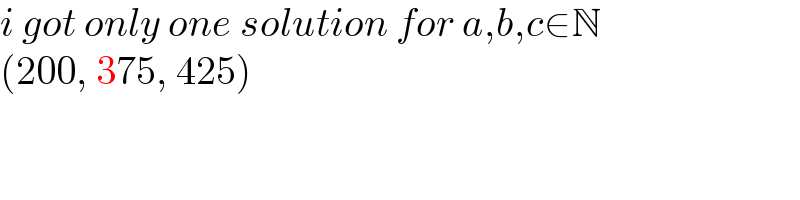
$${i}\:{got}\:{only}\:{one}\:{solution}\:{for}\:{a},{b},{c}\in\mathbb{N} \\ $$$$\left(\mathrm{200},\:\mathrm{375},\:\mathrm{425}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 22/Mar/22
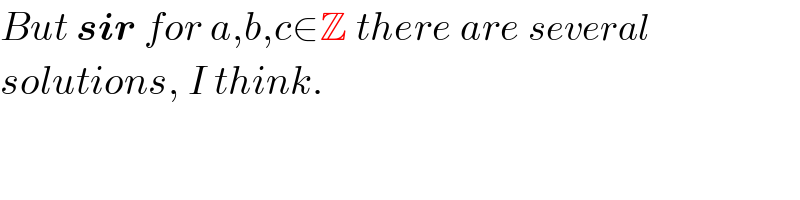
$${But}\:\boldsymbol{{sir}}\:{for}\:{a},{b},{c}\in\mathbb{Z}\:{there}\:{are}\:{several} \\ $$$${solutions},\:{I}\:{think}. \\ $$
Commented by Rasheed.Sindhi last updated on 22/Mar/22
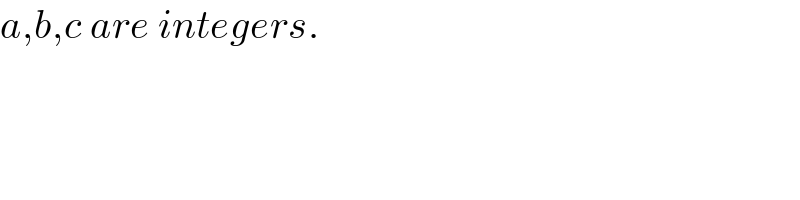
$${a},{b},{c}\:{are}\:{integers}. \\ $$
Answered by Rasheed.Sindhi last updated on 22/Mar/22
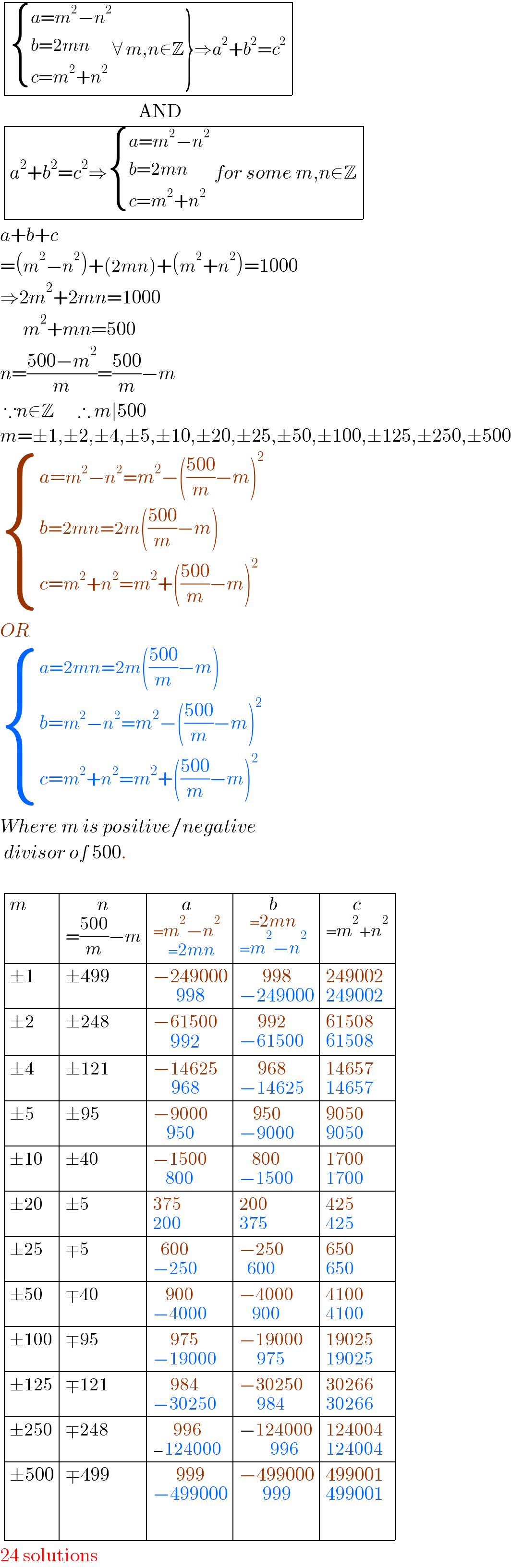
$$\begin{array}{|c|}{\left.\begin{cases}{{a}={m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\\{{b}=\mathrm{2}{mn}}\\{{c}={m}^{\mathrm{2}} +{n}^{\mathrm{2}} }\end{cases}\forall\:{m},{n}\in\mathbb{Z}\right\}\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} }\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{AND} \\ $$$$\begin{array}{|c|}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \Rightarrow\begin{cases}{{a}={m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\\{{b}=\mathrm{2}{mn}}\\{{c}={m}^{\mathrm{2}} +{n}^{\mathrm{2}} }\end{cases}\:{for}\:{some}\:{m},{n}\in\mathbb{Z}}\\\hline\end{array} \\ $$$${a}+{b}+{c} \\ $$$$=\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} \right)+\left(\mathrm{2}{mn}\right)+\left({m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)=\mathrm{1000} \\ $$$$\Rightarrow\mathrm{2}{m}^{\mathrm{2}} +\mathrm{2}{mn}=\mathrm{1000} \\ $$$$\:\:\:\:\:\:{m}^{\mathrm{2}} +{mn}=\mathrm{500} \\ $$$${n}=\frac{\mathrm{500}−{m}^{\mathrm{2}} }{{m}}=\frac{\mathrm{500}}{{m}}−{m} \\ $$$$\:\because{n}\in\mathbb{Z}\:\:\:\:\:\:\therefore\:{m}\mid\mathrm{500} \\ $$$${m}=\pm\mathrm{1},\pm\mathrm{2},\pm\mathrm{4},\pm\mathrm{5},\pm\mathrm{10},\pm\mathrm{20},\pm\mathrm{25},\pm\mathrm{50},\pm\mathrm{100},\pm\mathrm{125},\pm\mathrm{250},\pm\mathrm{500} \\ $$$$\begin{cases}{{a}={m}^{\mathrm{2}} −{n}^{\mathrm{2}} ={m}^{\mathrm{2}} −\left(\frac{\mathrm{500}}{{m}}−{m}\right)^{\mathrm{2}} }\\{{b}=\mathrm{2}{mn}=\mathrm{2}{m}\left(\frac{\mathrm{500}}{{m}}−{m}\right)}\\{{c}={m}^{\mathrm{2}} +{n}^{\mathrm{2}} ={m}^{\mathrm{2}} +\left(\frac{\mathrm{500}}{{m}}−{m}\right)^{\mathrm{2}} }\end{cases} \\ $$$${OR} \\ $$$$\begin{cases}{{a}=\mathrm{2}{mn}=\mathrm{2}{m}\left(\frac{\mathrm{500}}{{m}}−{m}\right)}\\{{b}={m}^{\mathrm{2}} −{n}^{\mathrm{2}} ={m}^{\mathrm{2}} −\left(\frac{\mathrm{500}}{{m}}−{m}\right)^{\mathrm{2}} }\\{{c}={m}^{\mathrm{2}} +{n}^{\mathrm{2}} ={m}^{\mathrm{2}} +\left(\frac{\mathrm{500}}{{m}}−{m}\right)^{\mathrm{2}} }\end{cases} \\ $$$${Where}\:{m}\:{is}\:{positive}/{negative} \\ $$$$\:{divisor}\:{of}\:\mathrm{500}. \\ $$$$ \\ $$$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}{{m}}&\hline{\underset{=\frac{\mathrm{500}}{{m}}−{m}} {{n}}}&\hline{\underset{=\underset{=\mathrm{2}{mn}} {{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }} {{a}}}&\hline{\underset{\underset{={m}^{\mathrm{2}} −{n}^{\mathrm{2}} } {=\mathrm{2}{mn}}} {{b}}}&\hline{\underset{={m}^{\mathrm{2}} +{n}^{\mathrm{2}} } {{c}}}\\{\pm\mathrm{1}}&\hline{\pm\mathrm{499}}&\hline{\underset{\mathrm{998}} {−\mathrm{249000}}}&\hline{\underset{−\mathrm{249000}} {\mathrm{998}}}&\hline{\underset{\mathrm{249002}} {\mathrm{249002}}}\\{\pm\mathrm{2}}&\hline{\pm\mathrm{248}}&\hline{\underset{\mathrm{992}} {−\mathrm{61500}}}&\hline{\underset{−\mathrm{61500}} {\mathrm{992}}}&\hline{\underset{\mathrm{61508}} {\mathrm{61508}}}\\{\pm\mathrm{4}}&\hline{\pm\mathrm{121}}&\hline{\underset{\mathrm{968}} {−\mathrm{14625}}}&\hline{\underset{−\mathrm{14625}} {\mathrm{968}}}&\hline{\underset{\mathrm{14657}} {\mathrm{14657}}}\\{\pm\mathrm{5}}&\hline{\pm\mathrm{95}}&\hline{\underset{\mathrm{950}} {−\mathrm{9000}}}&\hline{\underset{−\mathrm{9000}} {\mathrm{950}}}&\hline{\underset{\mathrm{9050}} {\mathrm{9050}}}\\{\pm\mathrm{10}}&\hline{\pm\mathrm{40}}&\hline{\underset{\mathrm{800}} {−\mathrm{1500}}}&\hline{\underset{−\mathrm{1500}} {\mathrm{800}}}&\hline{\underset{\mathrm{1700}} {\mathrm{1700}}}\\{\pm\mathrm{20}}&\hline{\pm\mathrm{5}}&\hline{\underset{\mathrm{200}} {\mathrm{375}}}&\hline{\underset{\mathrm{375}} {\mathrm{200}}}&\hline{\underset{\mathrm{425}} {\mathrm{425}}}\\{\pm\mathrm{25}}&\hline{\mp\mathrm{5}}&\hline{\underset{−\mathrm{250}} {\mathrm{600}}}&\hline{\underset{\mathrm{600}} {−\mathrm{250}}}&\hline{\underset{\mathrm{650}} {\mathrm{650}}}\\{\pm\mathrm{50}}&\hline{\mp\mathrm{40}}&\hline{\underset{−\mathrm{4000}} {\mathrm{900}}}&\hline{\underset{\mathrm{900}} {−\mathrm{4000}}}&\hline{\underset{\mathrm{4100}} {\mathrm{4100}}}\\{\pm\mathrm{100}}&\hline{\mp\mathrm{95}}&\hline{\underset{−\mathrm{19000}} {\mathrm{975}}}&\hline{\underset{\mathrm{975}} {−\mathrm{19000}}}&\hline{\underset{\mathrm{19025}} {\mathrm{19025}}}\\{\pm\mathrm{125}}&\hline{\mp\mathrm{121}}&\hline{\underset{−\mathrm{30250}} {\mathrm{984}}}&\hline{\underset{\mathrm{984}} {−\mathrm{30250}}}&\hline{\underset{\mathrm{30266}} {\mathrm{30266}}}\\{\pm\mathrm{250}}&\hline{\mp\mathrm{248}}&\hline{\underset{−\mathrm{124000}} {\mathrm{996}}}&\hline{−\underset{\mathrm{996}} {\mathrm{124000}}}&\hline{\underset{\mathrm{124004}} {\mathrm{124004}}}\\{\pm\mathrm{500}}&\hline{\mp\mathrm{499}}&\hline{\underset{−\mathrm{499000}} {\mathrm{999}}}&\hline{\underset{\mathrm{999}} {−\mathrm{499000}}}&\hline{\underset{\mathrm{499001}} {\mathrm{499001}}}\\\hline\end{array} \\ $$$$\mathrm{24}\:\mathrm{solutions} \\ $$
Commented by mr W last updated on 22/Mar/22

$${nice}\:{solution}! \\ $$
Commented by Rasheed.Sindhi last updated on 22/Mar/22

$$\begin{array}{|c|}{\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\boldsymbol{\mathrm{sir}}!}\\\hline\end{array} \\ $$
Commented by Tawa11 last updated on 22/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Mar/22

$$\:\begin{array}{|c|}{\underset{\mathcal{M}{iss}} {\mathcal{TH}\alpha{nk}\mathcal{S}}}\\\hline\end{array} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Mar/22
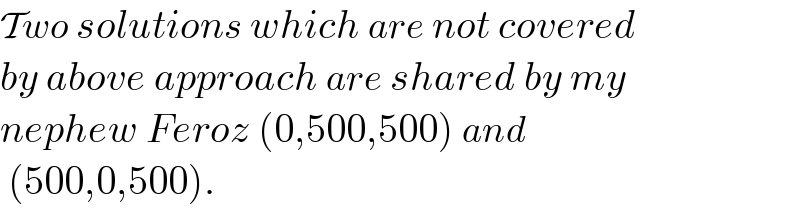
$$\mathcal{T}{wo}\:{solutions}\:{which}\:{are}\:{not}\:{covered} \\ $$$${by}\:{above}\:{approach}\:{are}\:{shared}\:{by}\:{my} \\ $$$${nephew}\:{Feroz}\:\left(\mathrm{0},\mathrm{500},\mathrm{500}\right)\:{and} \\ $$$$\:\left(\mathrm{500},\mathrm{0},\mathrm{500}\right). \\ $$
Commented by Rasheed.Sindhi last updated on 29/Mar/22
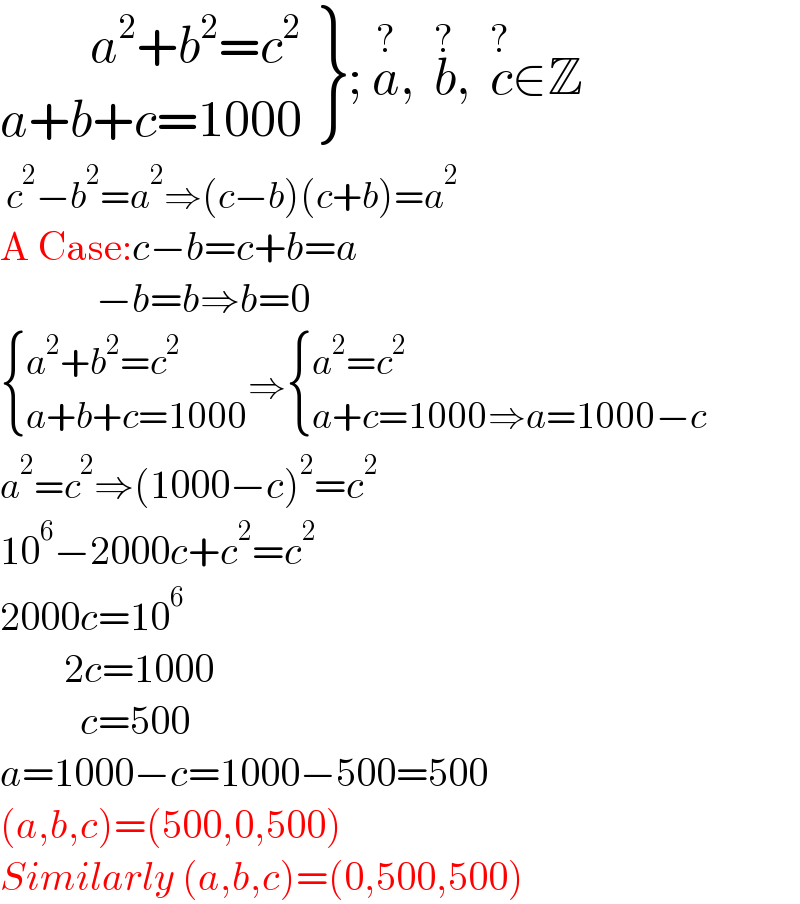
$$\left.\begin{matrix}{\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} }\\{{a}+{b}+{c}=\mathrm{1000}}\end{matrix}\right\};\:\overset{?} {{a}},\:\:\overset{?} {{b}},\:\:\overset{?} {{c}}\in\mathbb{Z} \\ $$$$\:{c}^{\mathrm{2}} −{b}^{\mathrm{2}} ={a}^{\mathrm{2}} \Rightarrow\left({c}−{b}\right)\left({c}+{b}\right)={a}^{\mathrm{2}} \\ $$$$\mathrm{A}\:\mathrm{Case}:{c}−{b}={c}+{b}={a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−{b}={b}\Rightarrow{b}=\mathrm{0} \\ $$$$\begin{cases}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} }\\{{a}+{b}+{c}=\mathrm{1000}}\end{cases}\Rightarrow\begin{cases}{{a}^{\mathrm{2}} ={c}^{\mathrm{2}} }\\{{a}+{c}=\mathrm{1000}\Rightarrow{a}=\mathrm{1000}−{c}}\end{cases}\: \\ $$$${a}^{\mathrm{2}} ={c}^{\mathrm{2}} \Rightarrow\left(\mathrm{1000}−{c}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\mathrm{10}^{\mathrm{6}} −\mathrm{2000}{c}+{c}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\mathrm{2000}{c}=\mathrm{10}^{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{c}=\mathrm{1000} \\ $$$$\:\:\:\:\:\:\:\:\:\:{c}=\mathrm{500} \\ $$$${a}=\mathrm{1000}−{c}=\mathrm{1000}−\mathrm{500}=\mathrm{500} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{500},\mathrm{0},\mathrm{500}\right) \\ $$$${Similarly}\:\left({a},{b},{c}\right)=\left(\mathrm{0},\mathrm{500},\mathrm{500}\right) \\ $$
