Question Number 157749 by naka3546 last updated on 27/Oct/21
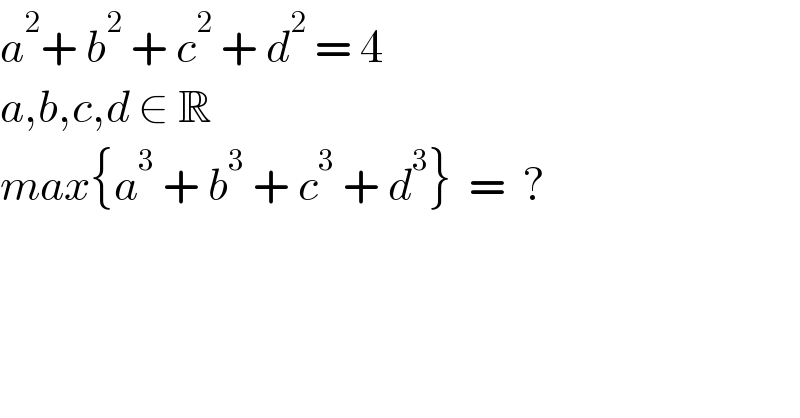
Commented by naka3546 last updated on 28/Oct/21
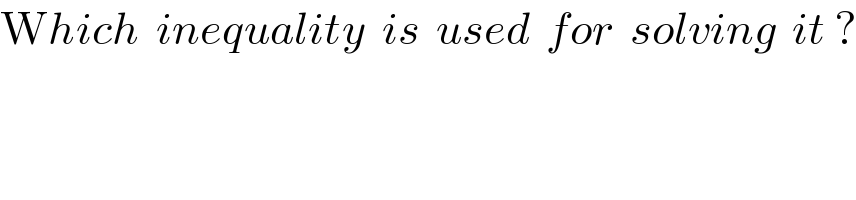
Commented by mr W last updated on 27/Oct/21

Commented by naka3546 last updated on 27/Oct/21
Commented by naka3546 last updated on 27/Oct/21
Commented by mr W last updated on 27/Oct/21
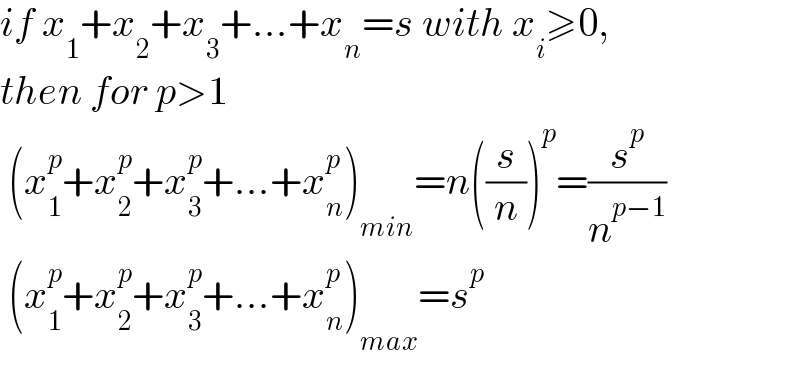
Commented by mr W last updated on 03/Aug/23
Commented by mr W last updated on 28/Oct/21

Commented by mr W last updated on 03/Aug/23
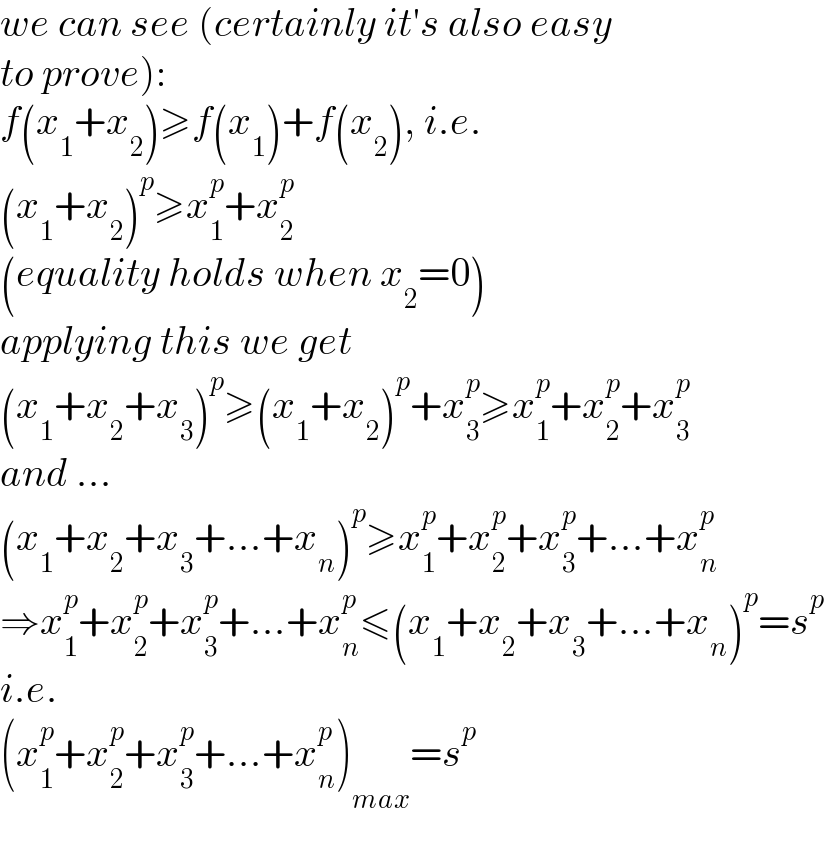
Commented by mr W last updated on 28/Oct/21
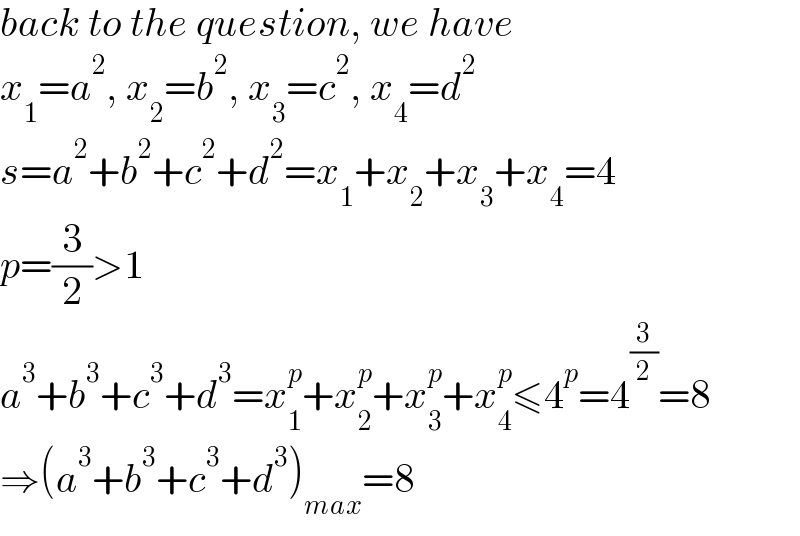
Commented by naka3546 last updated on 29/Oct/21