Question Number 149781 by mathdanisur last updated on 07/Aug/21

$$\mathrm{a}\:\:−\:\:\sqrt{\frac{\mathrm{20}}{\mathrm{a}}}\:=\:\mathrm{7}\:\:\Rightarrow\:\:\sqrt{\mathrm{5a}}\:−\:\mathrm{a}\:=\:? \\ $$
Commented by amin96 last updated on 07/Aug/21
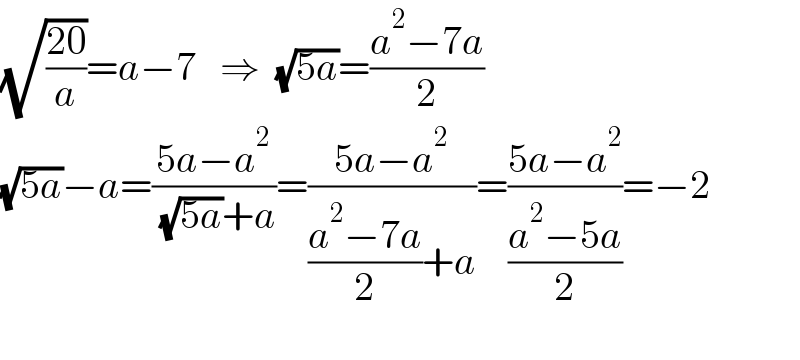
$$\sqrt{\frac{\mathrm{20}}{{a}}}={a}−\mathrm{7}\:\:\:\Rightarrow\:\:\sqrt{\mathrm{5}{a}}=\frac{{a}^{\mathrm{2}} −\mathrm{7}{a}}{\mathrm{2}}\:\: \\ $$$$\sqrt{\mathrm{5}{a}}−{a}=\frac{\mathrm{5}{a}−{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{5}{a}}+{a}}=\frac{\mathrm{5}{a}−{a}^{\mathrm{2}} }{\frac{{a}^{\mathrm{2}} −\mathrm{7}{a}}{\mathrm{2}}+{a}}=\frac{\mathrm{5}{a}−{a}^{\mathrm{2}} }{\frac{{a}^{\mathrm{2}} −\mathrm{5}{a}}{\mathrm{2}}}=−\mathrm{2} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 07/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by MJS_new last updated on 07/Aug/21
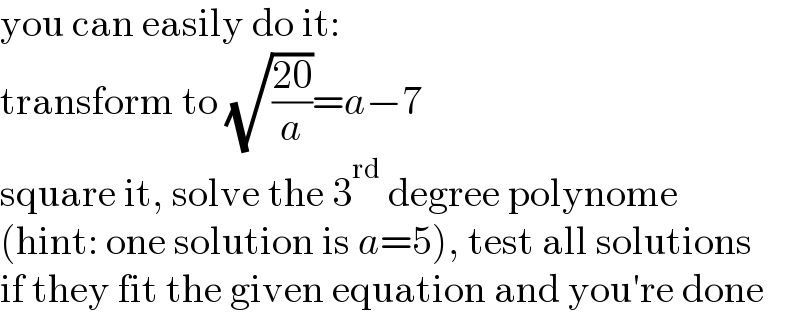
$$\mathrm{you}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{do}\:\mathrm{it}: \\ $$$$\mathrm{transform}\:\mathrm{to}\:\sqrt{\frac{\mathrm{20}}{{a}}}={a}−\mathrm{7} \\ $$$$\mathrm{square}\:\mathrm{it},\:\mathrm{solve}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{polynome} \\ $$$$\left(\mathrm{hint}:\:\mathrm{one}\:\mathrm{solution}\:\mathrm{is}\:{a}=\mathrm{5}\right),\:\mathrm{test}\:\mathrm{all}\:\mathrm{solutions} \\ $$$$\mathrm{if}\:\mathrm{they}\:\mathrm{fit}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{and}\:\mathrm{you}'\mathrm{re}\:\mathrm{done} \\ $$
