Menu Close

a-3-3ab-2-11-b-3-3a-2-b-2-a-b-R-a-2-b-2-

Tinku Tara 0 Comments
Pin




Question Number 176988 by cortano1 last updated on 29/Sep/22
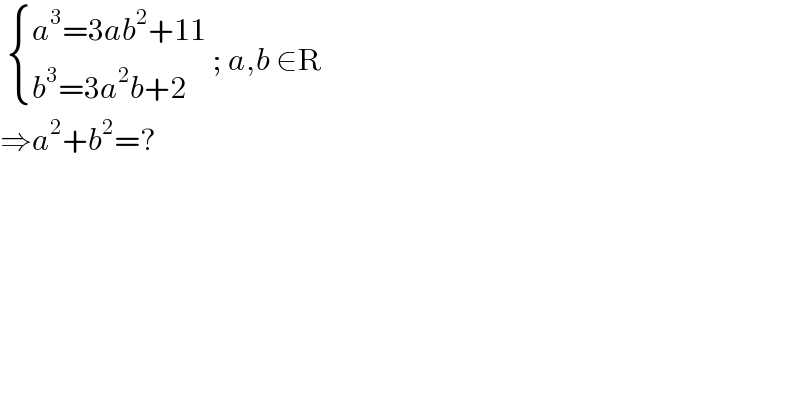
{ ((a^3 =3ab^2 +11)),((b^3 =3a^2 b+2)) :} ; a,b ∈R ⇒a^2 +b^2 =?
$$\:\begin{cases}{{a}^{\mathrm{3}} =\mathrm{3}{ab}^{\mathrm{2}} +\mathrm{11}}\\{{b}^{\mathrm{3}} =\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{2}}\end{cases}\:;\:{a},{b}\:\in\mathrm{R} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =? \\ $$
Commented by mr W last updated on 29/Sep/22
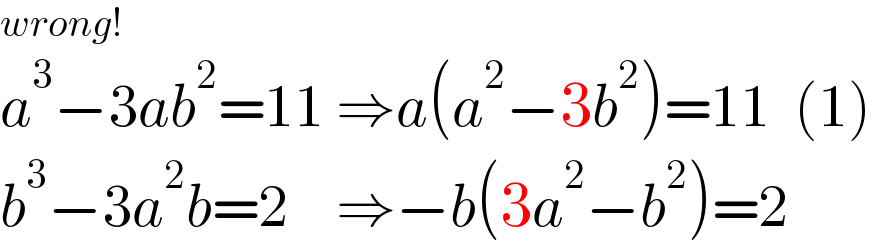
wrong! a^3 −3ab^2 =11 ⇒a(a^2 −3b^2 )=11 (1) b^3 −3a^2 b=2 ⇒−b(3a^2 −b^2 )=2
$${wrong}! \\ $$$${a}^{\mathrm{3}} −\mathrm{3}{ab}^{\mathrm{2}} =\mathrm{11}\:\Rightarrow{a}\left({a}^{\mathrm{2}} −\mathrm{3}{b}^{\mathrm{2}} \right)=\mathrm{11}\:\:\left(\mathrm{1}\right) \\ $$$${b}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {b}=\mathrm{2}\:\:\:\:\Rightarrow−{b}\left(\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=\mathrm{2} \\ $$
Commented by a.lgnaoui last updated on 29/Sep/22
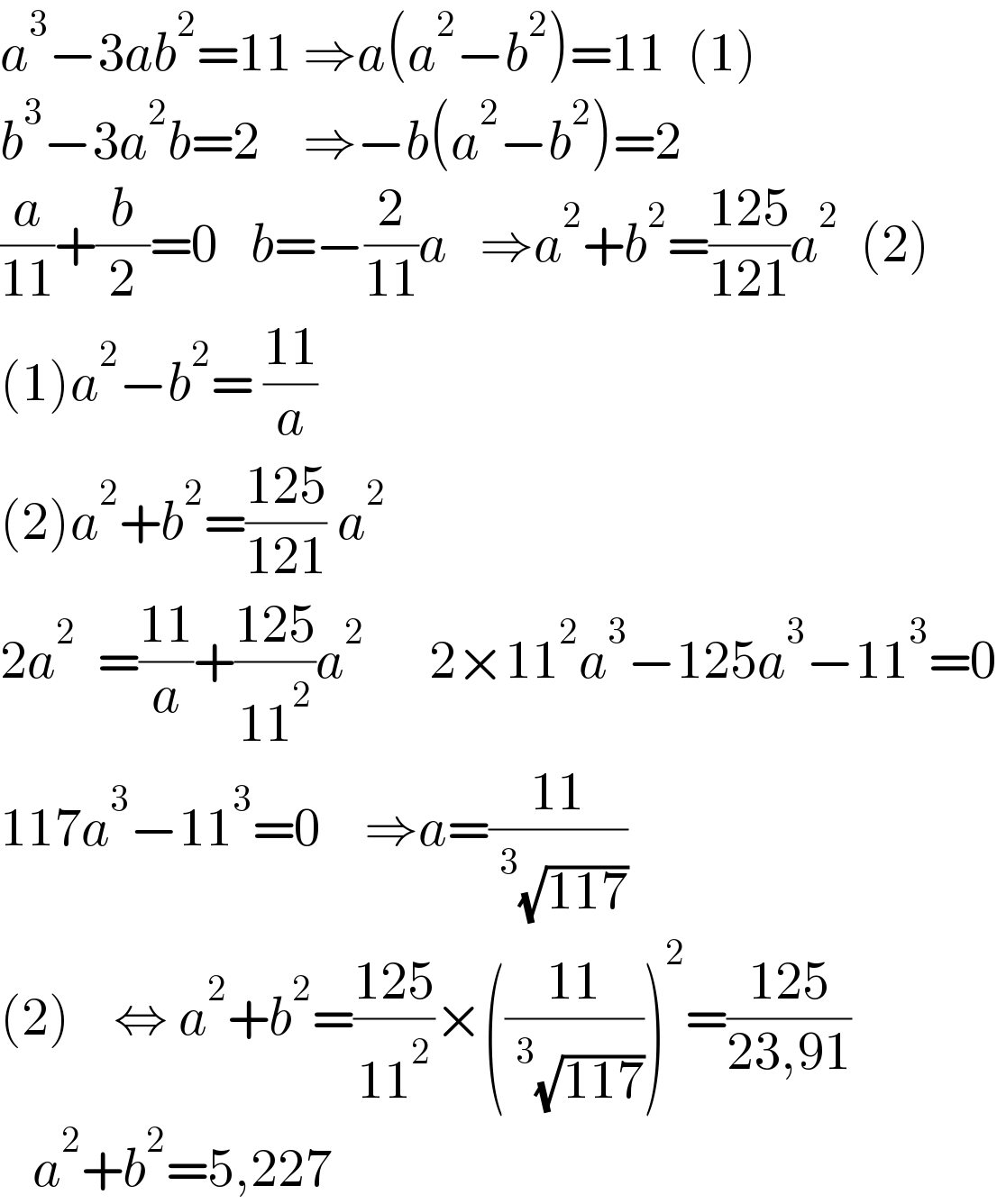
a^3 −3ab^2 =11 ⇒a(a^2 −b^2 )=11 (1) b^3 −3a^2 b=2 ⇒−b(a^2 −b^2 )=2 (a/(11))+(b/2)=0 b=−(2/(11))a ⇒a^2 +b^2 =((125)/(121))a^2 (2) (1)a^2 −b^2 = ((11)/a) (2)a^2 +b^2 =((125)/(121)) a^2 2a^2 =((11)/a)+((125)/(11^2 ))a^2 2×11^2 a^3 −125a^3 −11^3 =0 117a^3 −11^3 =0 ⇒a=((11)/(^3 (√(117)))) (2) ⇔ a^2 +b^2 =((125)/(11^2 ))×(((11)/(^3 (√(117)))))^2 =((125)/(23,91)) a^2 +b^2 =5,227
$${a}^{\mathrm{3}} −\mathrm{3}{ab}^{\mathrm{2}} =\mathrm{11}\:\Rightarrow{a}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=\mathrm{11}\:\:\left(\mathrm{1}\right) \\ $$$${b}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {b}=\mathrm{2}\:\:\:\:\Rightarrow−{b}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=\mathrm{2} \\ $$$$\frac{{a}}{\mathrm{11}}+\frac{{b}}{\mathrm{2}}=\mathrm{0}\:\:\:{b}=−\frac{\mathrm{2}}{\mathrm{11}}{a}\:\:\:\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{125}}{\mathrm{121}}{a}^{\mathrm{2}} \:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right){a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\:\frac{\mathrm{11}}{{a}}\:\:\:\: \\ $$$$\left(\mathrm{2}\right){a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{125}}{\mathrm{121}}\:{a}^{\mathrm{2}} \: \\ $$$$\mathrm{2}{a}^{\mathrm{2}} \:\:=\frac{\mathrm{11}}{{a}}+\frac{\mathrm{125}}{\mathrm{11}^{\mathrm{2}} }{a}^{\mathrm{2}} \:\:\:\:\:\:\mathrm{2}×\mathrm{11}^{\mathrm{2}} {a}^{\mathrm{3}} −\mathrm{125}{a}^{\mathrm{3}} −\mathrm{11}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{117}{a}^{\mathrm{3}} −\mathrm{11}^{\mathrm{3}} =\mathrm{0}\:\:\:\:\Rightarrow{a}=\frac{\mathrm{11}}{\:^{\mathrm{3}} \sqrt{\mathrm{117}}} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\Leftrightarrow\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{125}}{\mathrm{11}^{\mathrm{2}} }×\left(\frac{\mathrm{11}}{\:^{\mathrm{3}} \sqrt{\mathrm{117}}}\right)^{\mathrm{2}} =\frac{\mathrm{125}}{\mathrm{23},\mathrm{91}} \\ $$$$\:\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{5},\mathrm{227} \\ $$
Answered by blackmamba last updated on 29/Sep/22
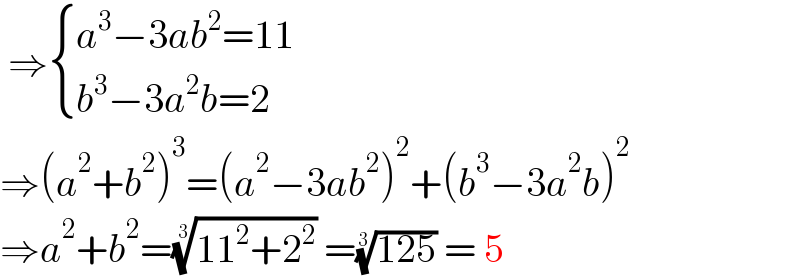
⇒ { ((a^3 −3ab^2 =11)),((b^3 −3a^2 b=2)) :} ⇒(a^2 +b^2 )^3 =(a^2 −3ab^2 )^2 +(b^3 −3a^2 b)^2 ⇒a^2 +b^2 =((11^2 +2^2 ))^(1/3) =((125))^(1/3) = 5
$$\:\Rightarrow\begin{cases}{{a}^{\mathrm{3}} −\mathrm{3}{ab}^{\mathrm{2}} =\mathrm{11}}\\{{b}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {b}=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{3}} =\left({a}^{\mathrm{2}} −\mathrm{3}{ab}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({b}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\sqrt[{\mathrm{3}}]{\mathrm{11}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:=\sqrt[{\mathrm{3}}]{\mathrm{125}}\:=\:\mathrm{5} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *