Question Number 31109 by naka3546 last updated on 02/Mar/18

$$\boldsymbol{{a}}^{\mathrm{4}} \:+\:\boldsymbol{{b}}^{\mathrm{4}} \:+\:\mathrm{13}\:\:\:{is}\:\:{a}\:\:{possible}\:\:{largest}\:\:{prime}\:\:{number}\:. \\ $$$$\boldsymbol{{a}}\:\:{and}\:\:\boldsymbol{{b}}\:\:{are}\:\:{prime}\:\:{numbers}\:. \\ $$$${Find}\:\:\boldsymbol{{a}}\:\:{and}\:\:\boldsymbol{{b}}\:. \\ $$
Commented by rahul 19 last updated on 02/Mar/18
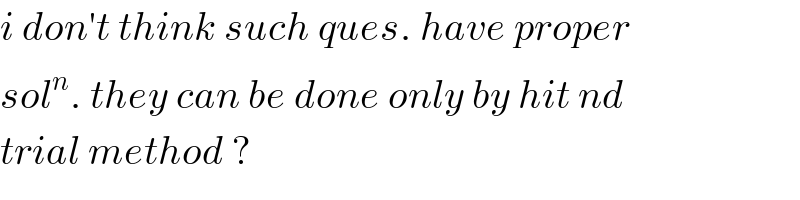
$${i}\:{don}'{t}\:{think}\:{such}\:{ques}.\:{have}\:{proper}\: \\ $$$${sol}^{{n}} .\:{they}\:{can}\:{be}\:{done}\:{only}\:{by}\:{hit}\:{nd} \\ $$$${trial}\:{method}\:? \\ $$
Commented by Tinkutara last updated on 02/Mar/18
Many of such questions indeed have a good thinking and proper logic. Many such questions can be solved by AOPS Community. I think posting questions there can help him.
Commented by MJS last updated on 03/Mar/18

$$\mathrm{what}\:\mathrm{does}\:“\mathrm{possible}\:\mathrm{largest}\:\mathrm{prime} \\ $$$$\mathrm{number}''\:\mathrm{mean}? \\ $$
Commented by naka3546 last updated on 04/Mar/18
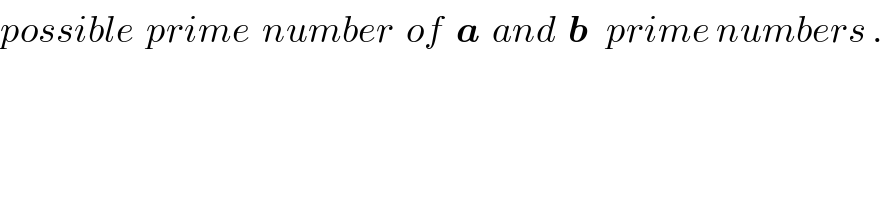
$${possible}\:\:{prime}\:\:{number}\:\:{of}\:\:\boldsymbol{{a}}\:\:{and}\:\:\boldsymbol{{b}}\:\:\:{prime}\:{numbers}\:. \\ $$
Commented by MJS last updated on 04/Mar/18
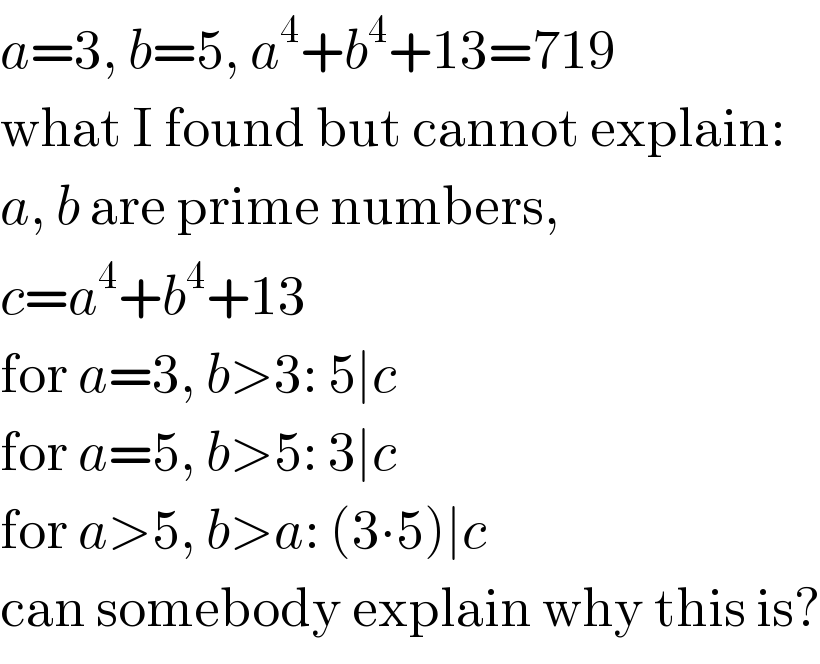
$${a}=\mathrm{3},\:{b}=\mathrm{5},\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +\mathrm{13}=\mathrm{719} \\ $$$$\mathrm{what}\:\mathrm{I}\:\mathrm{found}\:\mathrm{but}\:\mathrm{cannot}\:\mathrm{explain}: \\ $$$${a},\:{b}\:\mathrm{are}\:\mathrm{prime}\:\mathrm{numbers}, \\ $$$${c}={a}^{\mathrm{4}} +{b}^{\mathrm{4}} +\mathrm{13} \\ $$$$\mathrm{for}\:{a}=\mathrm{3},\:{b}>\mathrm{3}:\:\mathrm{5}\mid{c} \\ $$$$\mathrm{for}\:{a}=\mathrm{5},\:{b}>\mathrm{5}:\:\mathrm{3}\mid{c} \\ $$$$\mathrm{for}\:{a}>\mathrm{5},\:{b}>{a}:\:\left(\mathrm{3}\centerdot\mathrm{5}\right)\mid{c} \\ $$$$\mathrm{can}\:\mathrm{somebody}\:\mathrm{explain}\:\mathrm{why}\:\mathrm{this}\:\mathrm{is}? \\ $$
