Question Number 43496 by LYCON TRIX last updated on 11/Sep/18
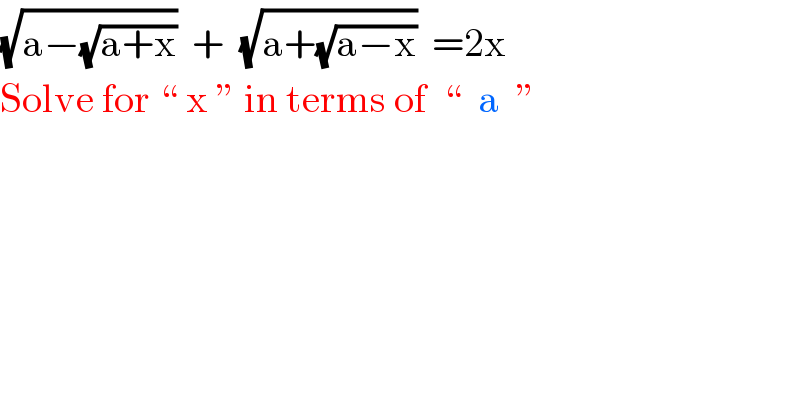
Commented by LYCON TRIX last updated on 11/Sep/18

Commented by LYCON TRIX last updated on 11/Sep/18
Commented by LYCON TRIX last updated on 11/Sep/18

Commented by LYCON TRIX last updated on 12/Sep/18
![I respect your efforts but , we want x in terms of a , moreover , x ∈ [ −a , +a ] so be careful](https://www.tinkutara.com/question/Q43564.png)
Answered by behi83417@gmail.com last updated on 12/Sep/18
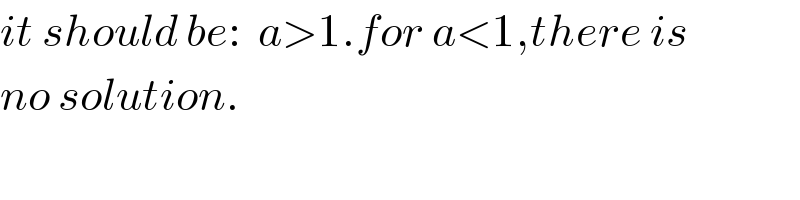
Commented by LYCON TRIX last updated on 12/Sep/18

Commented by behi83417@gmail.com last updated on 12/Sep/18