Menu Close

a-and-b-are-roots-of-this-equation-x-2018-2x-1-0-Calculate-the-value-of-2-a-b-a-2-b-2-a-3-b-3-a-2017-b-2017-

Tinku Tara 0 Comments
Pin




Question Number 58501 by naka3546 last updated on 24/Apr/19
a and b are roots of this equation : x^(2018) − 2x + 1 = 0 Calculate the value of 2 + (a+b) + (a^2 +b^2 ) + (a^3 + b^3 ) + … + (a^(2017) + b^(2017) )
$${a}\:\:{and}\:\:{b}\:\:{are}\:\:{roots}\:\:{of}\:\:{this}\:\:{equation}\:\:: \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2018}} \:−\:\mathrm{2}{x}\:+\:\mathrm{1}\:\:=\:\:\mathrm{0} \\ $$$${Calculate}\:\:{the}\:\:{value}\:\:\:{of} \\ $$$$\:\:\mathrm{2}\:+\:\left({a}+{b}\right)\:+\:\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\:+\:\left({a}^{\mathrm{3}} \:+\:{b}^{\mathrm{3}} \right)\:+\:\ldots\:+\:\left({a}^{\mathrm{2017}} \:+\:{b}^{\mathrm{2017}} \right) \\ $$
Answered by mr W last updated on 24/Apr/19
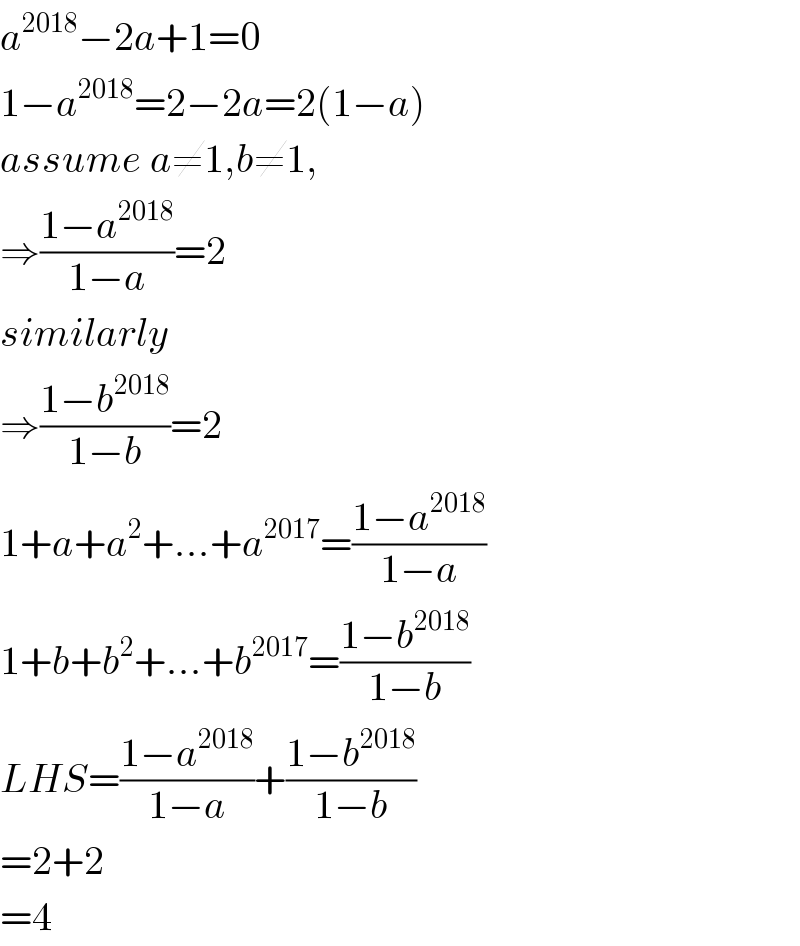
a^(2018) −2a+1=0 1−a^(2018) =2−2a=2(1−a) assume a≠1,b≠1, ⇒((1−a^(2018) )/(1−a))=2 similarly ⇒((1−b^(2018) )/(1−b))=2 1+a+a^2 +...+a^(2017) =((1−a^(2018) )/(1−a)) 1+b+b^2 +...+b^(2017) =((1−b^(2018) )/(1−b)) LHS=((1−a^(2018) )/(1−a))+((1−b^(2018) )/(1−b)) =2+2 =4
$${a}^{\mathrm{2018}} −\mathrm{2}{a}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{1}−{a}^{\mathrm{2018}} =\mathrm{2}−\mathrm{2}{a}=\mathrm{2}\left(\mathrm{1}−{a}\right) \\ $$$${assume}\:{a}\neq\mathrm{1},{b}\neq\mathrm{1}, \\ $$$$\Rightarrow\frac{\mathrm{1}−{a}^{\mathrm{2018}} }{\mathrm{1}−{a}}=\mathrm{2} \\ $$$${similarly} \\ $$$$\Rightarrow\frac{\mathrm{1}−{b}^{\mathrm{2018}} }{\mathrm{1}−{b}}=\mathrm{2} \\ $$$$\mathrm{1}+{a}+{a}^{\mathrm{2}} +…+{a}^{\mathrm{2017}} =\frac{\mathrm{1}−{a}^{\mathrm{2018}} }{\mathrm{1}−{a}} \\ $$$$\mathrm{1}+{b}+{b}^{\mathrm{2}} +…+{b}^{\mathrm{2017}} =\frac{\mathrm{1}−{b}^{\mathrm{2018}} }{\mathrm{1}−{b}} \\ $$$${LHS}=\frac{\mathrm{1}−{a}^{\mathrm{2018}} }{\mathrm{1}−{a}}+\frac{\mathrm{1}−{b}^{\mathrm{2018}} }{\mathrm{1}−{b}} \\ $$$$=\mathrm{2}+\mathrm{2} \\ $$$$=\mathrm{4} \\ $$
Commented by MJS last updated on 24/Apr/19
but one root of x^(2n) −2x+1=0 is 1
$$\mathrm{but}\:\mathrm{one}\:\mathrm{root}\:\mathrm{of}\:{x}^{\mathrm{2}{n}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0}\:\mathrm{is}\:\mathrm{1} \\ $$
Commented by mr W last updated on 24/Apr/19
yes sir. one root is x=1, but there are 2017 further roots which are not equal to 1. i only treated those roots. if a=1 (or b=1) my solution is not valid.
$${yes}\:{sir}.\:{one}\:{root}\:{is}\:{x}=\mathrm{1},\:{but}\:{there} \\ $$$${are}\:\mathrm{2017}\:{further}\:{roots}\:{which}\:{are} \\ $$$${not}\:{equal}\:{to}\:\mathrm{1}.\:{i}\:{only}\:{treated}\:{those} \\ $$$${roots}.\:{if}\:{a}=\mathrm{1}\:\left({or}\:{b}=\mathrm{1}\right)\:{my}\:{solution} \\ $$$${is}\:{not}\:{valid}. \\ $$
Answered by MJS last updated on 24/Apr/19
x^(2n) −2x+1=(x−1)(x^(2n−1) +x^(2n−2) +...+x−1) ⇒ x^(2n−1) +x^(2n−2) +...+x+1=2 a=1∧b=x (1^0 +x^0 )+(1^1 +x^1 )+...+(1^(2n−1) +x^(2n−1) )= =2n+2 in our case 2n=2018 ⇒ 2n+2=2020
$${x}^{\mathrm{2}{n}} −\mathrm{2}{x}+\mathrm{1}=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}{n}−\mathrm{1}} +{x}^{\mathrm{2}{n}−\mathrm{2}} +…+{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\:{x}^{\mathrm{2}{n}−\mathrm{1}} +{x}^{\mathrm{2}{n}−\mathrm{2}} +…+{x}+\mathrm{1}=\mathrm{2} \\ $$$${a}=\mathrm{1}\wedge{b}={x} \\ $$$$\left(\mathrm{1}^{\mathrm{0}} +{x}^{\mathrm{0}} \right)+\left(\mathrm{1}^{\mathrm{1}} +{x}^{\mathrm{1}} \right)+…+\left(\mathrm{1}^{\mathrm{2}{n}−\mathrm{1}} +{x}^{\mathrm{2}{n}−\mathrm{1}} \right)= \\ $$$$=\mathrm{2}{n}+\mathrm{2} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:\mathrm{2}{n}=\mathrm{2018}\:\Rightarrow\:\mathrm{2}{n}+\mathrm{2}=\mathrm{2020} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *