Question Number 171941 by infinityaction last updated on 22/Jun/22

$$\sqrt{{a}}+\sqrt{{b}}=\sqrt{\mathrm{2009}}.\:{find}\:{a}\:{and}\:{b}. \\ $$
Commented by infinityaction last updated on 22/Jun/22

$${repost}\:{of}\:{que}.\:{no}\:\mathrm{171866} \\ $$
Commented by infinityaction last updated on 22/Jun/22
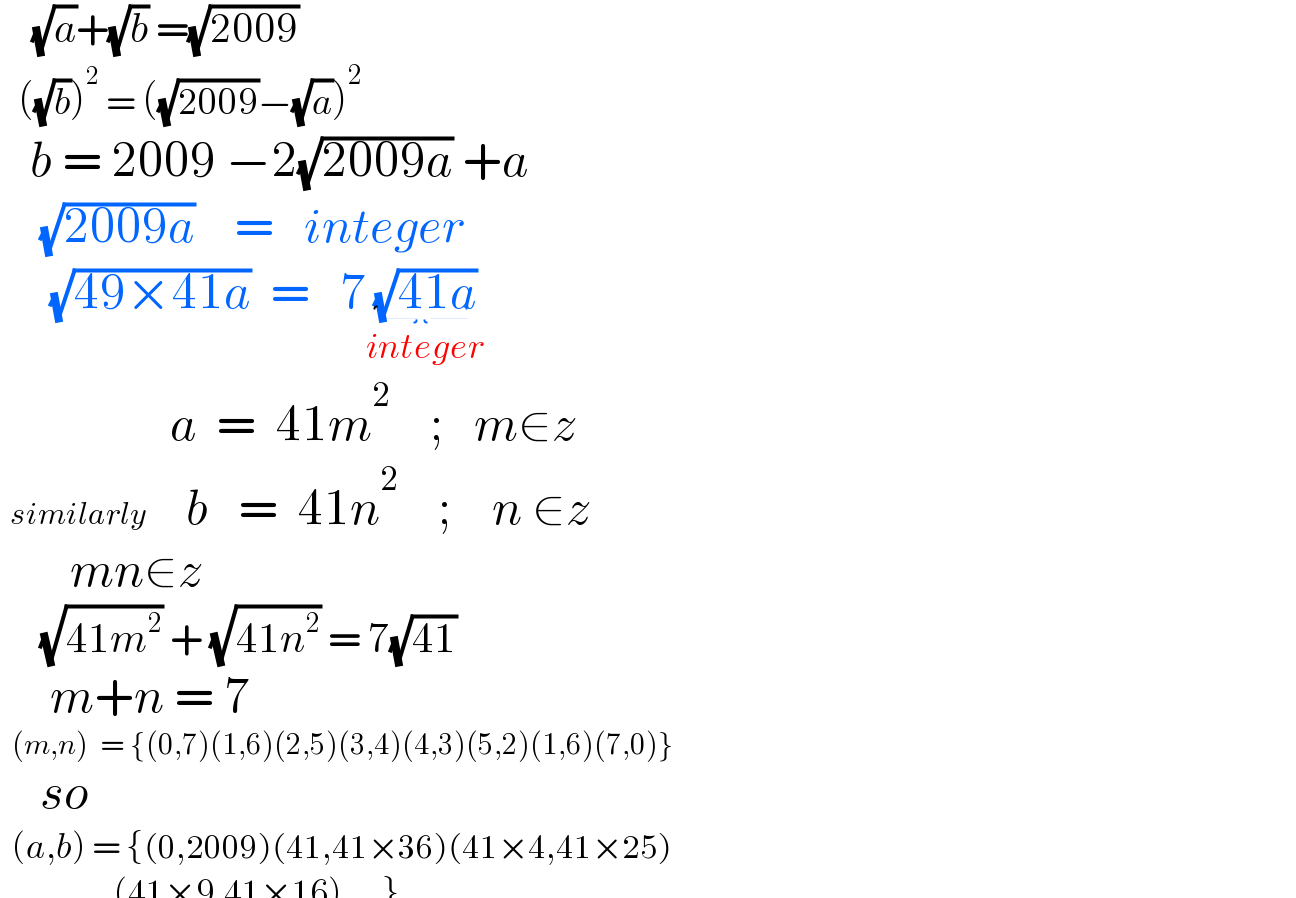
$$\:\:\:\:\sqrt{{a}}+\sqrt{{b}}\:=\sqrt{\mathrm{2009}} \\ $$$$\:\:\:\left(\sqrt{{b}}\right)^{\mathrm{2}} \:=\:\left(\sqrt{\mathrm{2009}}−\sqrt{{a}}\right)^{\mathrm{2}} \\ $$$$\:\:\:{b}\:=\:\mathrm{2009}\:−\mathrm{2}\sqrt{\mathrm{2009}{a}}\:+{a} \\ $$$$\:\:\:\:\sqrt{\mathrm{2009}{a}}\:\:\:\:=\:\:\:{integer} \\ $$$$\:\:\:\:\:\sqrt{\mathrm{49}×\mathrm{41}{a}}\:\:=\:\:\:\mathrm{7}\underset{{integer}} {\underbrace{\sqrt{\mathrm{41}{a}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\:\:=\:\:\mathrm{41}{m}^{\mathrm{2}} \:\:\:\:;\:\:\:{m}\in{z} \\ $$$$\:{similarly}\:\:\:\:{b}\:\:\:=\:\:\mathrm{41}{n}^{\mathrm{2}} \:\:\:\:;\:\:\:\:{n}\:\in{z} \\ $$$$\:\:\:\:\:\:\:{mn}\in{z} \\ $$$$\:\:\:\:\:\sqrt{\mathrm{41}{m}^{\mathrm{2}} }\:+\:\sqrt{\mathrm{41}{n}^{\mathrm{2}} }\:=\:\mathrm{7}\sqrt{\mathrm{41}} \\ $$$$\:\:\:\:\:{m}+{n}\:=\:\mathrm{7} \\ $$$$\:\:\left({m},{n}\right)\:\:=\:\left\{\left(\mathrm{0},\mathrm{7}\right)\left(\mathrm{1},\mathrm{6}\right)\left(\mathrm{2},\mathrm{5}\right)\left(\mathrm{3},\mathrm{4}\right)\left(\mathrm{4},\mathrm{3}\right)\left(\mathrm{5},\mathrm{2}\right)\left(\mathrm{1},\mathrm{6}\right)\left(\mathrm{7},\mathrm{0}\right)\right\} \\ $$$$\:\:\:\:{so} \\ $$$$\:\:\left({a},{b}\right)\:=\:\left\{\left(\mathrm{0},\mathrm{2009}\right)\left(\mathrm{41},\mathrm{41}×\mathrm{36}\right)\left(\mathrm{41}×\mathrm{4},\mathrm{41}×\mathrm{25}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{41}×\mathrm{9},\mathrm{41}×\mathrm{16}\right)….\right\} \\ $$
Commented by Mikenice last updated on 23/Jun/22

$${thanks}\:{sir} \\ $$
