Question Number 28695 by yesaditya22@gmail.com last updated on 29/Jan/18
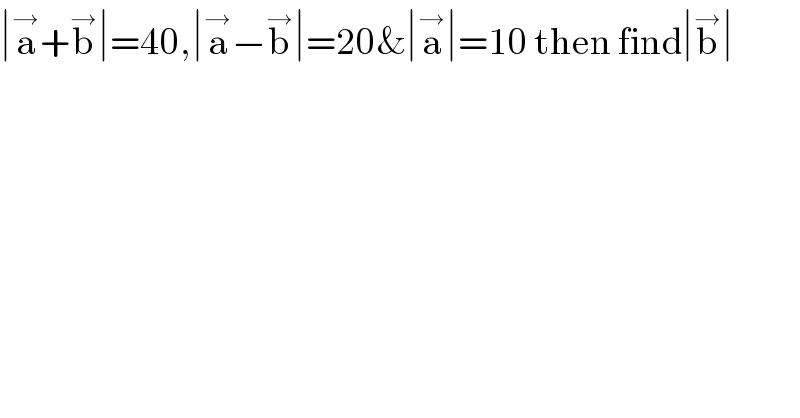
$$\mid\overset{\rightarrow} {\mathrm{a}}+\overset{\rightarrow} {\mathrm{b}}\mid=\mathrm{40},\mid\overset{\rightarrow} {\mathrm{a}}−\overset{\rightarrow} {\mathrm{b}}\mid=\mathrm{20\&}\mid\overset{\rightarrow} {\mathrm{a}}\mid=\mathrm{10}\:\mathrm{then}\:\mathrm{find}\mid\overset{\rightarrow} {\mathrm{b}}\mid \\ $$
Answered by mrW2 last updated on 29/Jan/18
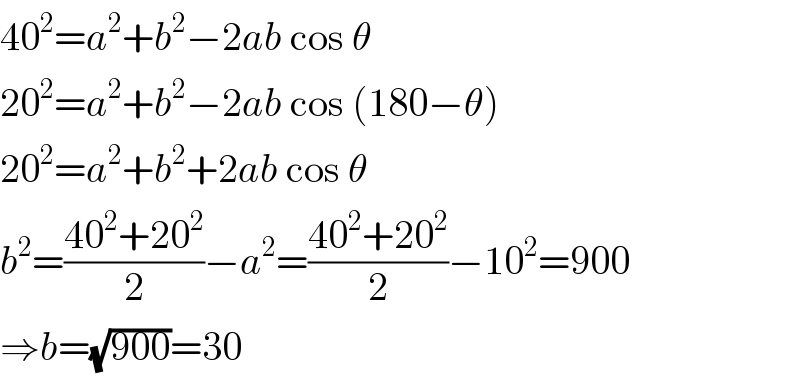
$$\mathrm{40}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{20}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\left(\mathrm{180}−\theta\right) \\ $$$$\mathrm{20}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\theta \\ $$$${b}^{\mathrm{2}} =\frac{\mathrm{40}^{\mathrm{2}} +\mathrm{20}^{\mathrm{2}} }{\mathrm{2}}−{a}^{\mathrm{2}} =\frac{\mathrm{40}^{\mathrm{2}} +\mathrm{20}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{10}^{\mathrm{2}} =\mathrm{900} \\ $$$$\Rightarrow{b}=\sqrt{\mathrm{900}}=\mathrm{30} \\ $$
