Question Number 87313 by mr W last updated on 03/Apr/20
$${a},{b},{c}=\mathrm{1},\mathrm{2},\mathrm{3},…,{n} \\ $$$${find}\:\underset{{a}\neq{b}\neq{c}} {\sum}{abc} \\ $$
Commented by mr W last updated on 04/Apr/20
$${yes},\:{you}\:{are}\:{right}. \\ $$
Commented by mr W last updated on 04/Apr/20
$${for}\:{example}\:{n}=\mathrm{4} \\ $$$$\underset{{a}\neq{b}\neq{c}} {\sum}{abc}=\mathrm{1}×\mathrm{2}×\mathrm{3}+\mathrm{1}×\mathrm{2}×\mathrm{4}+\mathrm{1}×\mathrm{3}×\mathrm{4}+\mathrm{2}×\mathrm{3}×\mathrm{4}=\mathrm{50} \\ $$
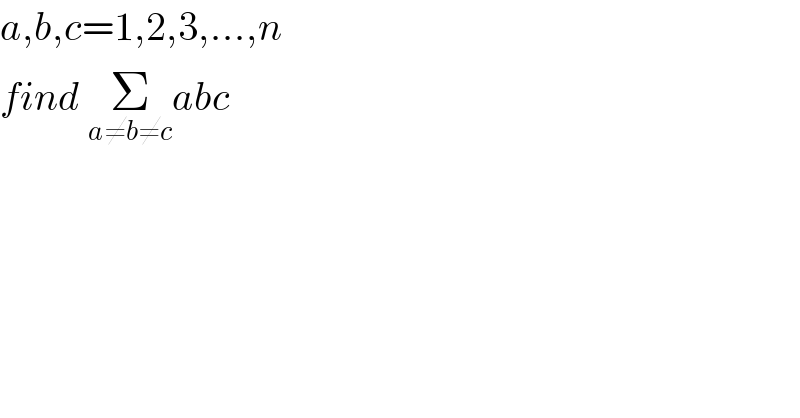
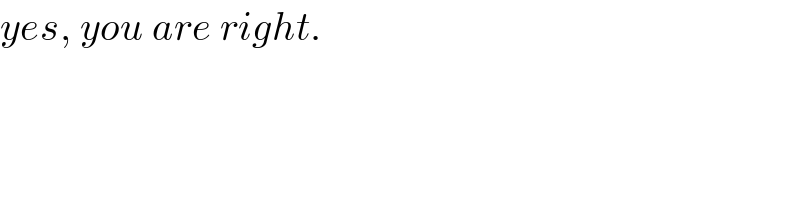
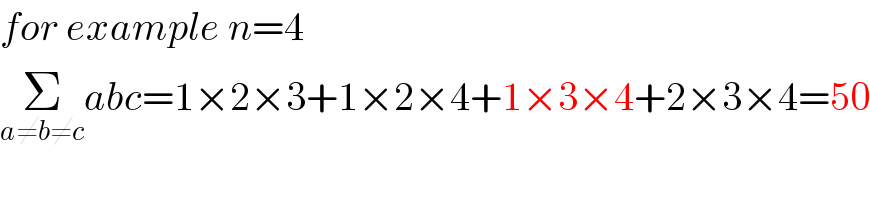
Commented by mr W last updated on 03/Apr/20
$${to}\:{choose}\:{three}\:{different}\:{numbers} \\ $$$${from}\:{n}\:{numbers}\:{there}\:{are}\:{C}_{\mathrm{3}} ^{{n}} \: \\ $$$${combinations}.\:{from}\:{each}\:{combination} \\ $$$${we}\:{get}\:{the}\:{product}\:{of}\:{the}\:{three}\:{numbers}. \\ $$$${now}\:{it}\:{is}\:{to}\:{find}\:{the}\:{sum}\:{of}\:{all}\:{these} \\ $$$${products}. \\ $$
Commented by MJS last updated on 04/Apr/20
$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{for}\:{n}=\mathrm{4}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{1}×\mathrm{2}×\mathrm{3}+\mathrm{1}×\mathrm{2}×\mathrm{4}+\mathrm{1}×\mathrm{3}×\mathrm{4}+\mathrm{2}×\mathrm{3}×\mathrm{4}=\mathrm{50} \\ $$
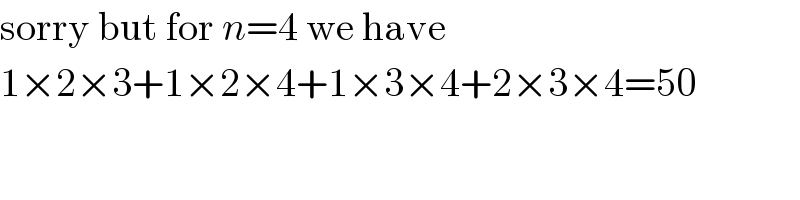
Answered by mr W last updated on 04/Apr/20
![S=Σabc=(Σ_(a=1) ^n a)(Σ_(b=1) ^n b)(Σ_(c=1) ^n c)=[((n(n+1))/2)]^3 S_1 =Σ_(a=b=c) abc=Σ_(a=1) ^n a^3 =((n^2 (n+1)^2 )/4) S_2 =Σ_(a,b=c≠a) abc=3Σ_(b=1) ^n [(Σ_(a=1) ^n a−b)(b^2 )] =3Σ_(b=1) ^n [(Σ_(a=1) ^n a)b^2 −b^3 ] =3[(Σ_(a=1) ^n a)(Σ_(b=1) ^n b^2 )−(Σ_(b=1) ^n b^3 )] =3[((n(n+1))/2)×((n(n+1)(2n+1))/6)−((n^2 (n+1)^2 )/4)] =(((n−1)n^2 (n+1)^2 )/2) S_3 =Σ_(a≠b≠c) abc=(1/(3!))(S−S_1 −S_2 ) =(1/6)[((n^3 (n+1)^3 )/8)−((n^2 (n+1)^2 )/4)−(((n−1)n^2 (n+1)^2 )/2)] =(((n−2)(n−1)n^2 (n+1)^2 )/(48)) example: n=4 S_3 =((2×3×4^2 ×5^2 )/(48))=50 1×2×3+1×2×4+1×3×4+2×3×3 =50 example: n=5 S_3 =((3×4×5^2 ×6^2 )/(48))=225 1×2×3+1×2×4+1×2×5+1×3×4+1×3×5+1×4×5 +2×3×4+2×3×5 +3×4×5 =225](https://www.tinkutara.com/question/Q87368.png)
$${S}=\Sigma{abc}=\left(\underset{{a}=\mathrm{1}} {\overset{{n}} {\sum}}{a}\right)\left(\underset{{b}=\mathrm{1}} {\overset{{n}} {\sum}}{b}\right)\left(\underset{{c}=\mathrm{1}} {\overset{{n}} {\sum}}{c}\right)=\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right]^{\mathrm{3}} \\ $$$$ \\ $$$${S}_{\mathrm{1}} =\underset{{a}={b}={c}} {\sum}{abc}=\underset{{a}=\mathrm{1}} {\overset{{n}} {\sum}}{a}^{\mathrm{3}} =\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$$${S}_{\mathrm{2}} =\underset{{a},{b}={c}\neq{a}} {\sum}{abc}=\mathrm{3}\underset{{b}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\left(\underset{{a}=\mathrm{1}} {\overset{{n}} {\sum}}{a}−{b}\right)\left({b}^{\mathrm{2}} \right)\right] \\ $$$$=\mathrm{3}\underset{{b}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\left(\underset{{a}=\mathrm{1}} {\overset{{n}} {\sum}}{a}\right){b}^{\mathrm{2}} −{b}^{\mathrm{3}} \right] \\ $$$$=\mathrm{3}\left[\left(\underset{{a}=\mathrm{1}} {\overset{{n}} {\sum}}{a}\right)\left(\underset{{b}=\mathrm{1}} {\overset{{n}} {\sum}}{b}^{\mathrm{2}} \right)−\left(\underset{{b}=\mathrm{1}} {\overset{{n}} {\sum}}{b}^{\mathrm{3}} \right)\right] \\ $$$$=\mathrm{3}\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}×\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}−\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\right] \\ $$$$=\frac{\left({n}−\mathrm{1}\right){n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$$${S}_{\mathrm{3}} =\underset{{a}\neq{b}\neq{c}} {\sum}{abc}=\frac{\mathrm{1}}{\mathrm{3}!}\left({S}−{S}_{\mathrm{1}} −{S}_{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{{n}^{\mathrm{3}} \left({n}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{8}}−\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{\left({n}−\mathrm{1}\right){n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\right] \\ $$$$=\frac{\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right){n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{48}} \\ $$$$ \\ $$$${example}:\:{n}=\mathrm{4} \\ $$$${S}_{\mathrm{3}} =\frac{\mathrm{2}×\mathrm{3}×\mathrm{4}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} }{\mathrm{48}}=\mathrm{50} \\ $$$$\mathrm{1}×\mathrm{2}×\mathrm{3}+\mathrm{1}×\mathrm{2}×\mathrm{4}+\mathrm{1}×\mathrm{3}×\mathrm{4}+\mathrm{2}×\mathrm{3}×\mathrm{3} \\ $$$$=\mathrm{50} \\ $$$$ \\ $$$${example}:\:{n}=\mathrm{5} \\ $$$${S}_{\mathrm{3}} =\frac{\mathrm{3}×\mathrm{4}×\mathrm{5}^{\mathrm{2}} ×\mathrm{6}^{\mathrm{2}} }{\mathrm{48}}=\mathrm{225} \\ $$$$\mathrm{1}×\mathrm{2}×\mathrm{3}+\mathrm{1}×\mathrm{2}×\mathrm{4}+\mathrm{1}×\mathrm{2}×\mathrm{5}+\mathrm{1}×\mathrm{3}×\mathrm{4}+\mathrm{1}×\mathrm{3}×\mathrm{5}+\mathrm{1}×\mathrm{4}×\mathrm{5} \\ $$$$+\mathrm{2}×\mathrm{3}×\mathrm{4}+\mathrm{2}×\mathrm{3}×\mathrm{5} \\ $$$$+\mathrm{3}×\mathrm{4}×\mathrm{5} \\ $$$$=\mathrm{225} \\ $$