Question Number 147076 by mathdanisur last updated on 17/Jul/21
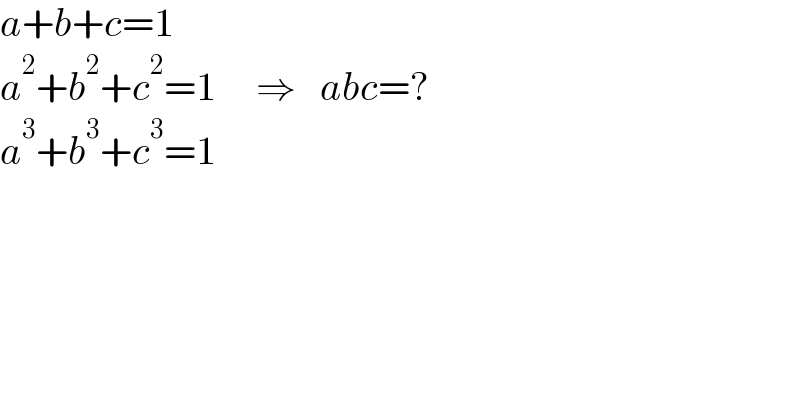
$${a}+{b}+{c}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:\Rightarrow\:\:\:{abc}=? \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{1} \\ $$
Answered by gsk2684 last updated on 17/Jul/21
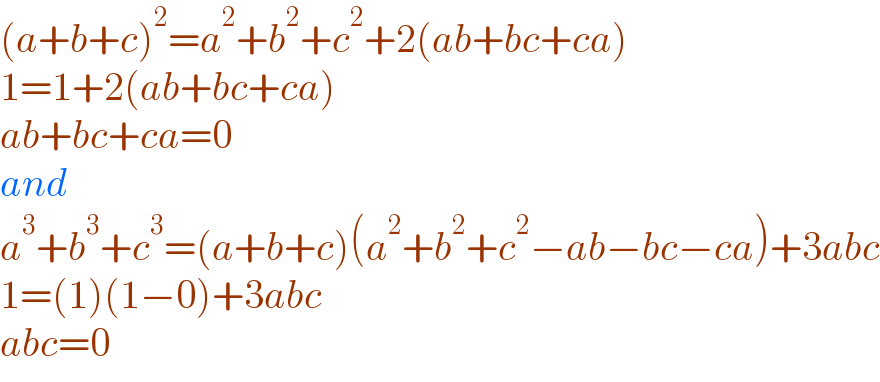
$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\mathrm{1}=\mathrm{1}+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${ab}+{bc}+{ca}=\mathrm{0} \\ $$$${and} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)+\mathrm{3}{abc} \\ $$$$\mathrm{1}=\left(\mathrm{1}\right)\left(\mathrm{1}−\mathrm{0}\right)+\mathrm{3}{abc} \\ $$$${abc}=\mathrm{0} \\ $$
Commented by mathdanisur last updated on 18/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
Answered by mr W last updated on 17/Jul/21
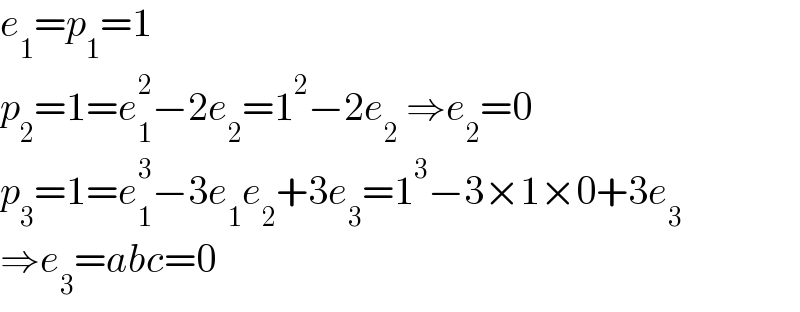
$${e}_{\mathrm{1}} ={p}_{\mathrm{1}} =\mathrm{1} \\ $$$${p}_{\mathrm{2}} =\mathrm{1}={e}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{e}_{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} −\mathrm{2}{e}_{\mathrm{2}} \:\Rightarrow{e}_{\mathrm{2}} =\mathrm{0} \\ $$$${p}_{\mathrm{3}} =\mathrm{1}={e}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{3}{e}_{\mathrm{1}} {e}_{\mathrm{2}} +\mathrm{3}{e}_{\mathrm{3}} =\mathrm{1}^{\mathrm{3}} −\mathrm{3}×\mathrm{1}×\mathrm{0}+\mathrm{3}{e}_{\mathrm{3}} \\ $$$$\Rightarrow{e}_{\mathrm{3}} ={abc}=\mathrm{0} \\ $$
Commented by mathdanisur last updated on 18/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
