Question Number 32841 by alimudinade@gmail.com last updated on 03/Apr/18
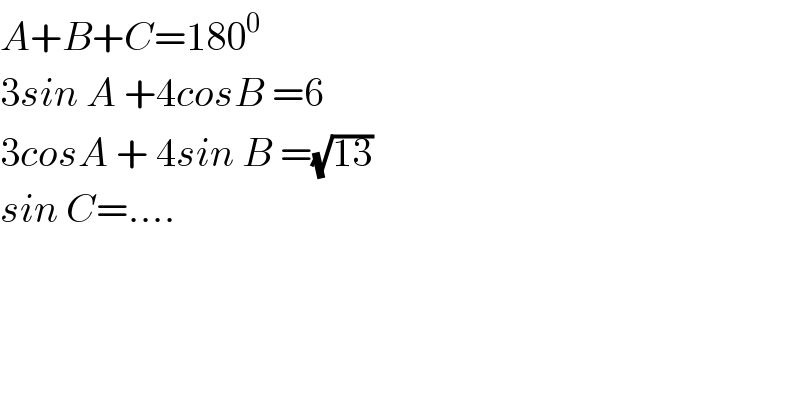
$${A}+{B}+{C}=\mathrm{180}^{\mathrm{0}} \\ $$$$\mathrm{3}{sin}\:{A}\:+\mathrm{4}{cosB}\:=\mathrm{6} \\ $$$$\mathrm{3}{cosA}\:+\:\mathrm{4}{sin}\:{B}\:=\sqrt{\mathrm{13}} \\ $$$${sin}\:{C}=…. \\ $$
Answered by hknkrc46 last updated on 04/Apr/18

$$\mathrm{36}+\mathrm{13}=\mathrm{49} \\ $$$$\left(\mathrm{3sinA}+\mathrm{4cosB}\right)^{\mathrm{2}} +\left(\mathrm{3cosA}+\mathrm{4sinB}\right)^{\mathrm{2}} =\mathrm{49} \\ $$$$\mathrm{9}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{cos}^{\mathrm{2}} \mathrm{A}\right)+\mathrm{16}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{B}+\mathrm{cos}^{\mathrm{2}} \mathrm{B}\right)+\mathrm{24sin}\left(\mathrm{A}+\mathrm{B}\right)=\mathrm{49} \\ $$$$\mathrm{9}+\mathrm{16}+\mathrm{24sin}\left(\mathrm{180}−\mathrm{C}\right)=\mathrm{49} \\ $$$$\mathrm{24sinC}=\mathrm{24} \\ $$$$\mathrm{sinC}=\mathrm{1} \\ $$$$ \\ $$
