Question Number 42224 by 33 last updated on 20/Aug/18

Commented by rahul 19 last updated on 20/Aug/18
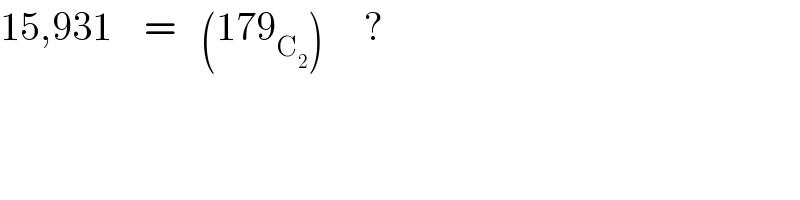
Commented by 33 last updated on 20/Aug/18

Commented by rahul 19 last updated on 20/Aug/18

Commented by 33 last updated on 20/Aug/18
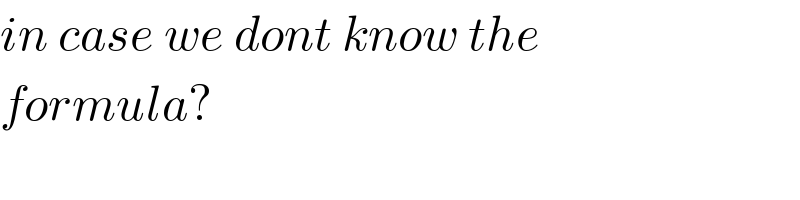
Commented by Tinkutara last updated on 20/Aug/18
See Q. 22040
