Question Number 54603 by behi83417@gmail.com last updated on 07/Feb/19
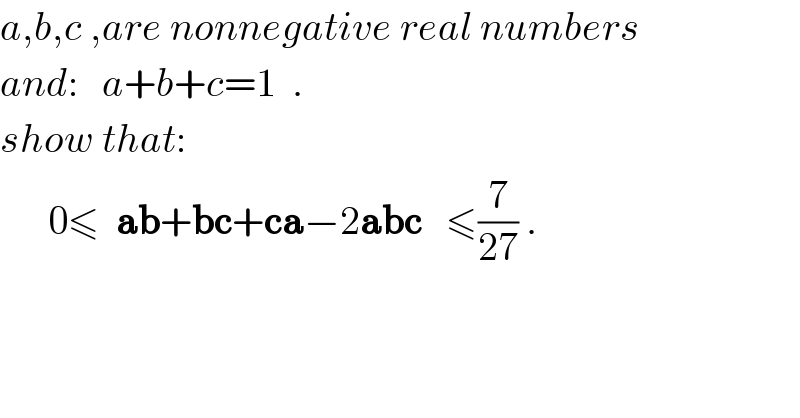
$${a},{b},{c}\:,{are}\:{nonnegative}\:{real}\:{numbers} \\ $$$${and}:\:\:\:{a}+{b}+{c}=\mathrm{1}\:\:. \\ $$$${show}\:{that}: \\ $$$$\:\:\:\:\:\:\mathrm{0}\leqslant\:\:\boldsymbol{\mathrm{ab}}+\boldsymbol{\mathrm{bc}}+\boldsymbol{\mathrm{ca}}−\mathrm{2}\boldsymbol{\mathrm{abc}}\:\:\:\leqslant\frac{\mathrm{7}}{\mathrm{27}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 08/Feb/19
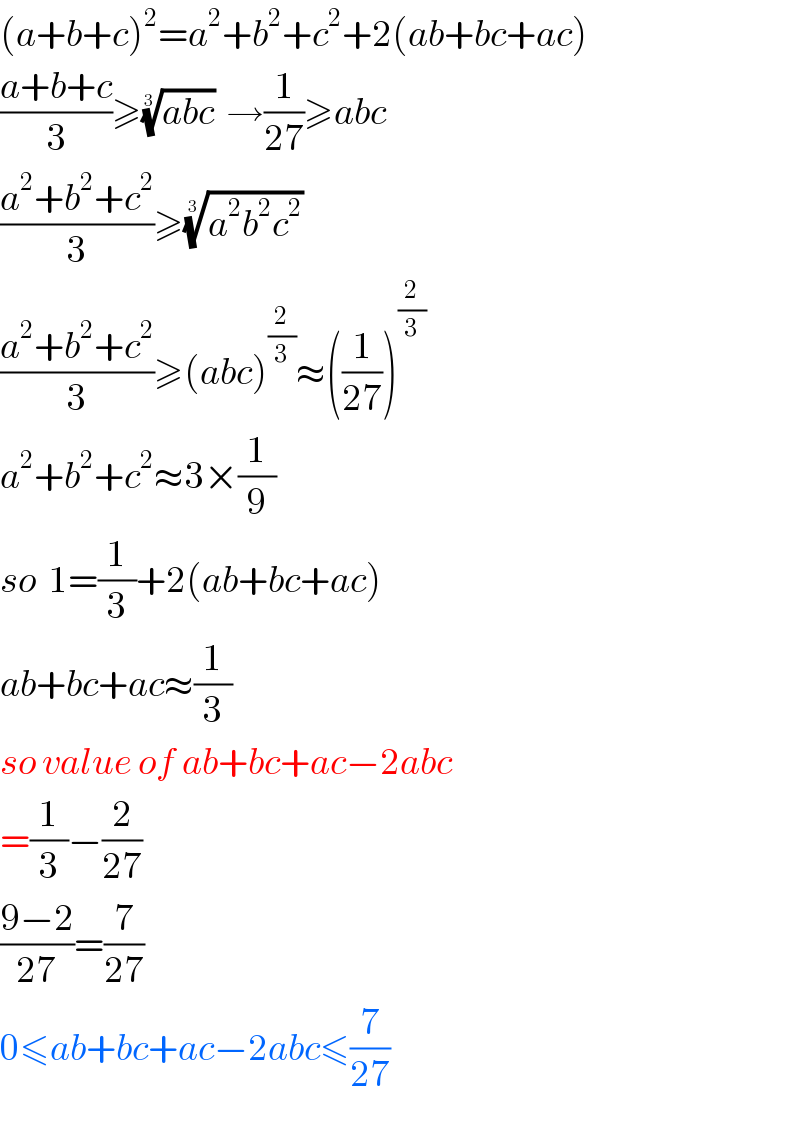
$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ac}\right) \\ $$$$\frac{{a}+{b}+{c}}{\mathrm{3}}\geqslant\sqrt[{\mathrm{3}}]{{abc}}\:\:\rightarrow\frac{\mathrm{1}}{\mathrm{27}}\geqslant{abc} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}\geqslant\sqrt[{\mathrm{3}}]{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} } \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}\geqslant\left({abc}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \approx\left(\frac{\mathrm{1}}{\mathrm{27}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \approx\mathrm{3}×\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${so}\:\:\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{2}\left({ab}+{bc}+{ac}\right) \\ $$$${ab}+{bc}+{ac}\approx\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${so}\:{value}\:{of}\:{ab}+{bc}+{ac}−\mathrm{2}{abc} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{27}} \\ $$$$\frac{\mathrm{9}−\mathrm{2}}{\mathrm{27}}=\frac{\mathrm{7}}{\mathrm{27}} \\ $$$$\mathrm{0}\leqslant{ab}+{bc}+{ac}−\mathrm{2}{abc}\leqslant\frac{\mathrm{7}}{\mathrm{27}} \\ $$
