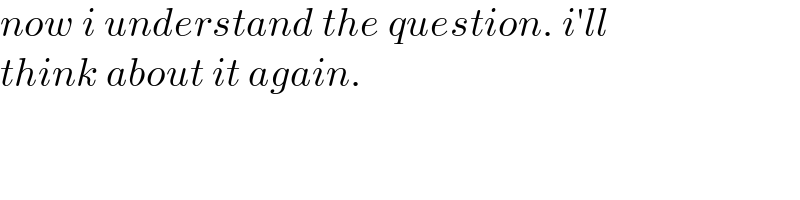Question Number 155797 by ajfour last updated on 09/Oct/21
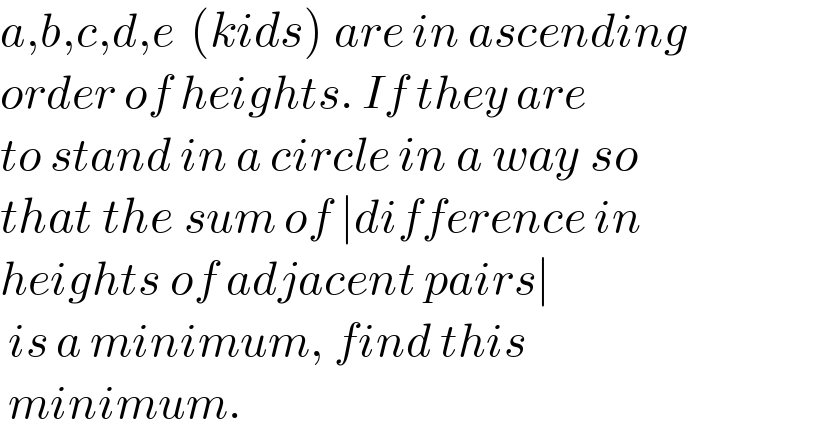
Commented by ajfour last updated on 09/Oct/21
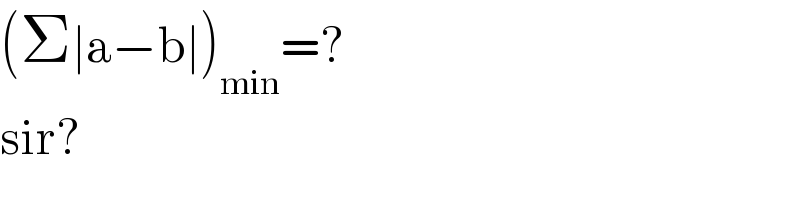
Commented by mr W last updated on 05/Oct/21
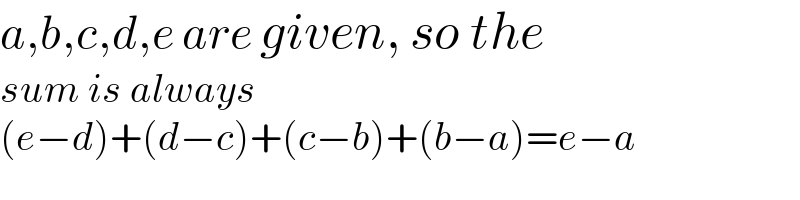
Commented by mr W last updated on 05/Oct/21
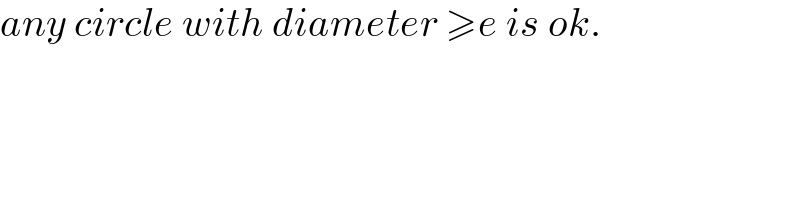
Commented by mr W last updated on 09/Oct/21
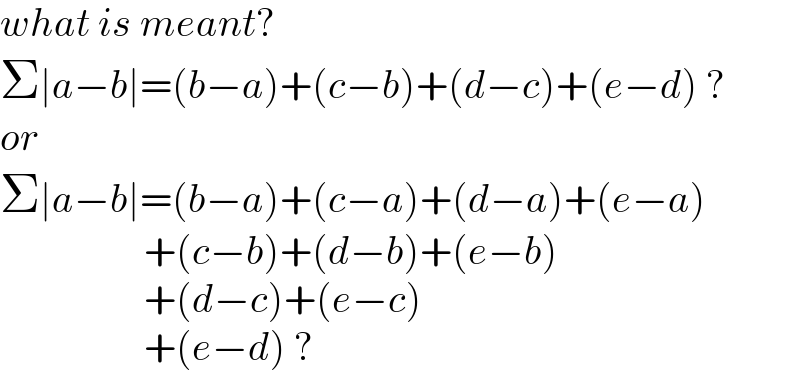
Commented by ajfour last updated on 09/Oct/21
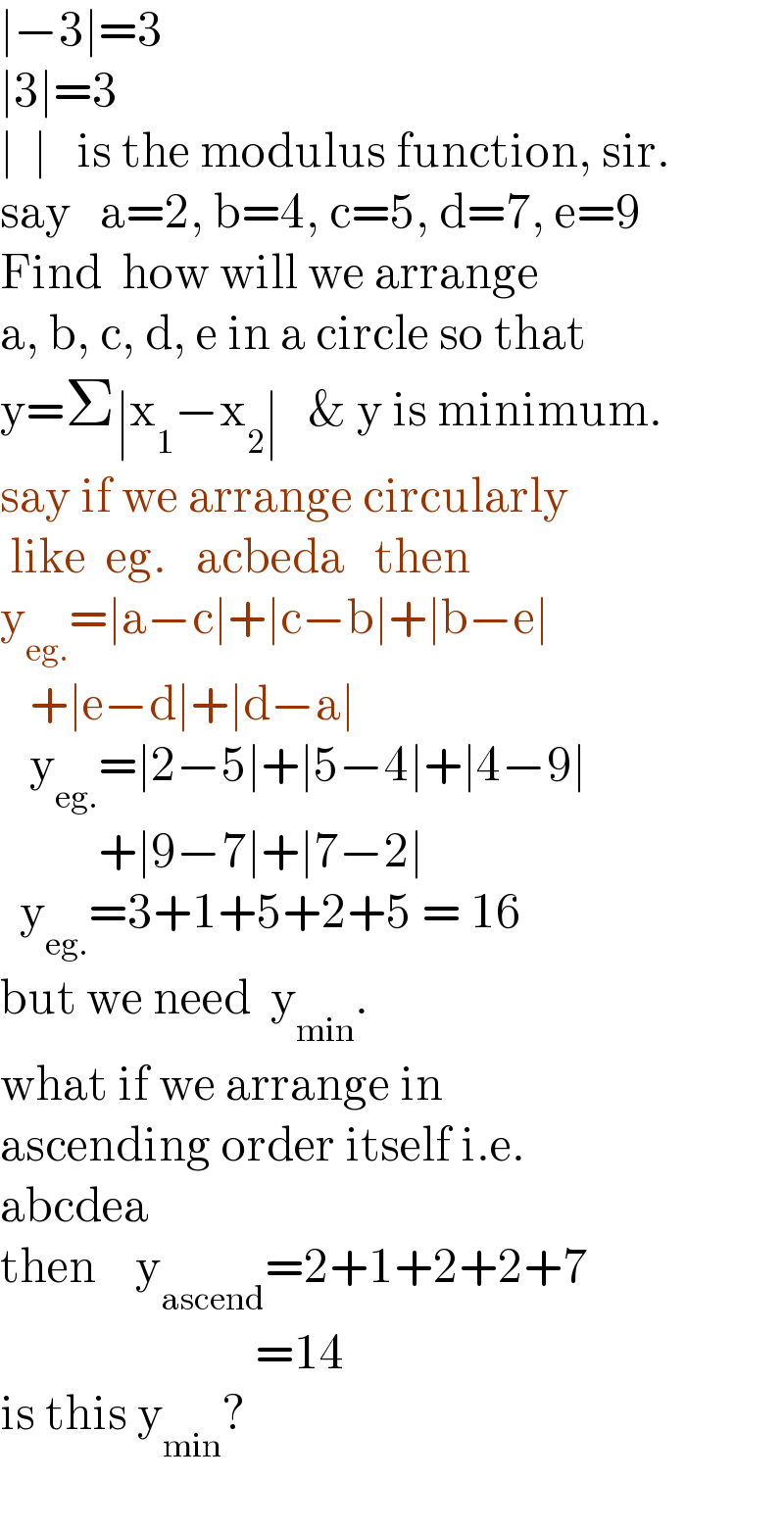
Commented by mr W last updated on 09/Oct/21