Question Number 151371 by mathdanisur last updated on 20/Aug/21
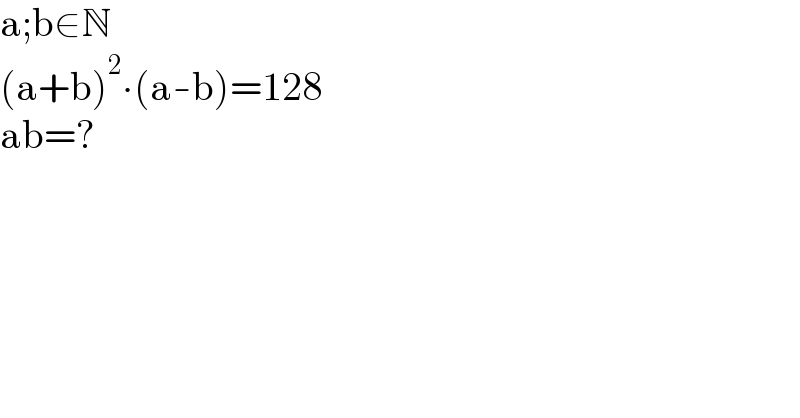
$$\mathrm{a};\mathrm{b}\in\mathbb{N} \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \centerdot\left(\mathrm{a}-\mathrm{b}\right)=\mathrm{128} \\ $$$$\mathrm{ab}=? \\ $$
Answered by nimnim last updated on 20/Aug/21
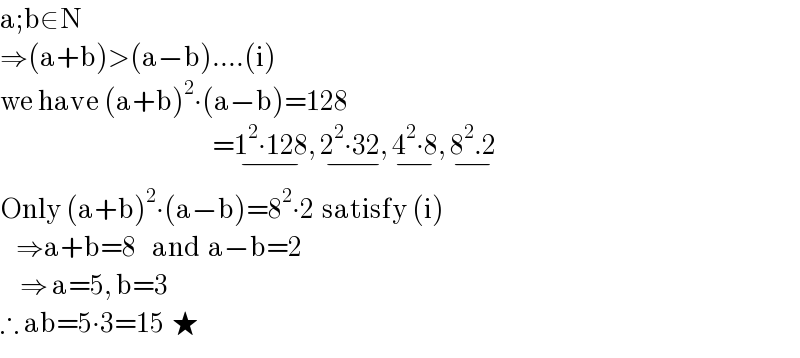
$$\mathrm{a};\mathrm{b}\in\mathrm{N} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)>\left(\mathrm{a}−\mathrm{b}\right)….\left(\mathrm{i}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \centerdot\left(\mathrm{a}−\mathrm{b}\right)=\mathrm{128} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{−} {\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{128}},\:\underset{−} {\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{32},}\:\underset{−} {\mathrm{4}^{\mathrm{2}} \centerdot\mathrm{8}},\:\underset{−} {\mathrm{8}^{\mathrm{2}} .\mathrm{2}} \\ $$$$\mathrm{Only}\:\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \centerdot\left(\mathrm{a}−\mathrm{b}\right)=\mathrm{8}^{\mathrm{2}} \centerdot\mathrm{2}\:\:\mathrm{satisfy}\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{8}\:\:\:\:\mathrm{and}\:\:\mathrm{a}−\mathrm{b}=\mathrm{2} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{a}=\mathrm{5},\:\mathrm{b}=\mathrm{3} \\ $$$$\therefore\:\mathrm{ab}=\mathrm{5}\centerdot\mathrm{3}=\mathrm{15}\:\:\bigstar \\ $$
