Question Number 47607 by tanmay.chaudhury50@gmail.com last updated on 12/Nov/18

$$\int_{{a}} ^{{b}} \frac{\mid{x}\mid}{{x}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 12/Nov/18
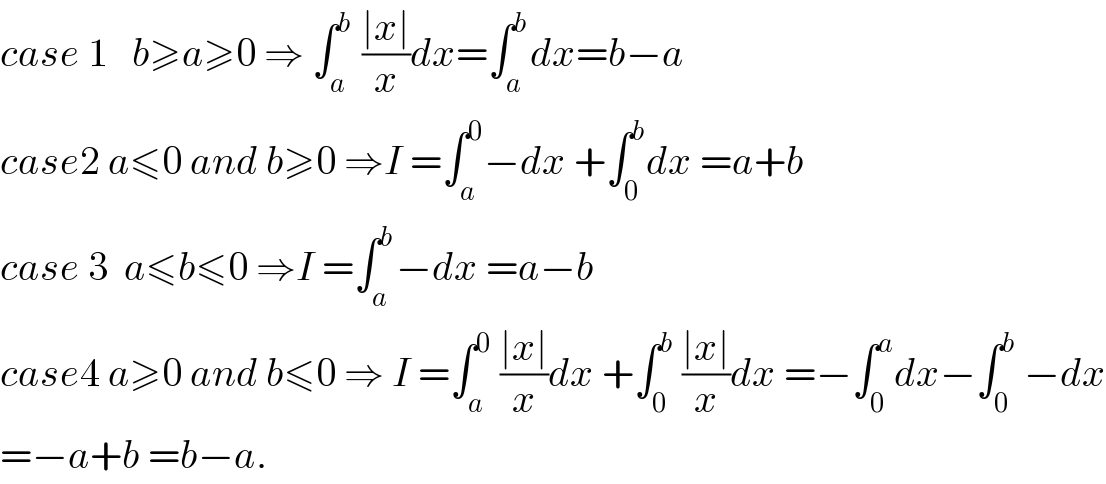
$${case}\:\mathrm{1}\:\:\:{b}\geqslant{a}\geqslant\mathrm{0}\:\Rightarrow\:\int_{{a}} ^{{b}} \:\frac{\mid{x}\mid}{{x}}{dx}=\int_{{a}} ^{{b}} {dx}={b}−{a} \\ $$$${case}\mathrm{2}\:{a}\leqslant\mathrm{0}\:{and}\:{b}\geqslant\mathrm{0}\:\Rightarrow{I}\:=\int_{{a}} ^{\mathrm{0}} −{dx}\:+\int_{\mathrm{0}} ^{{b}} {dx}\:={a}+{b} \\ $$$${case}\:\mathrm{3}\:\:{a}\leqslant{b}\leqslant\mathrm{0}\:\Rightarrow{I}\:=\int_{{a}} ^{{b}} −{dx}\:={a}−{b} \\ $$$${case}\mathrm{4}\:{a}\geqslant\mathrm{0}\:{and}\:{b}\leqslant\mathrm{0}\:\Rightarrow\:{I}\:=\int_{{a}} ^{\mathrm{0}} \:\frac{\mid{x}\mid}{{x}}{dx}\:+\int_{\mathrm{0}} ^{{b}} \:\frac{\mid{x}\mid}{{x}}{dx}\:=−\int_{\mathrm{0}} ^{{a}} {dx}−\int_{\mathrm{0}} ^{{b}} \:−{dx} \\ $$$$=−{a}+{b}\:={b}−{a}. \\ $$
Answered by ajfour last updated on 12/Nov/18
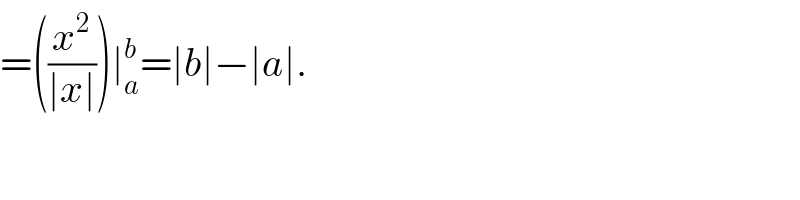
$$=\left(\frac{{x}^{\mathrm{2}} }{\mid{x}\mid}\right)\mid_{{a}} ^{{b}} =\mid{b}\mid−\mid{a}\mid. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Nov/18

$${excellent}… \\ $$
