Question Number 111163 by Aina Samuel Temidayo last updated on 02/Sep/20

$$\mathrm{A}\:\mathrm{bag}\:\mathrm{contains}\:\mathrm{11}\:\mathrm{white}\:\mathrm{balls}\:\mathrm{and}\:\mathrm{9} \\ $$$$\mathrm{black}\:\mathrm{balls},\:\mathrm{another}\:\mathrm{contains}\:\mathrm{12}\:\mathrm{white} \\ $$$$\mathrm{balls}\:\mathrm{and}\:\mathrm{13}\:\mathrm{black}\:\mathrm{balls}.\:\mathrm{If}\:\mathrm{two}\:\mathrm{balls} \\ $$$$\mathrm{are}\:\mathrm{drawn}\:\mathrm{without}\:\mathrm{replacement},\:\mathrm{from} \\ $$$$\mathrm{each}\:\mathrm{bag}\:\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that} \\ $$$$\mathrm{exactly}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{4}\:\mathrm{balls}\:\mathrm{is}\:\mathrm{white}? \\ $$
Commented by Aina Samuel Temidayo last updated on 02/Sep/20
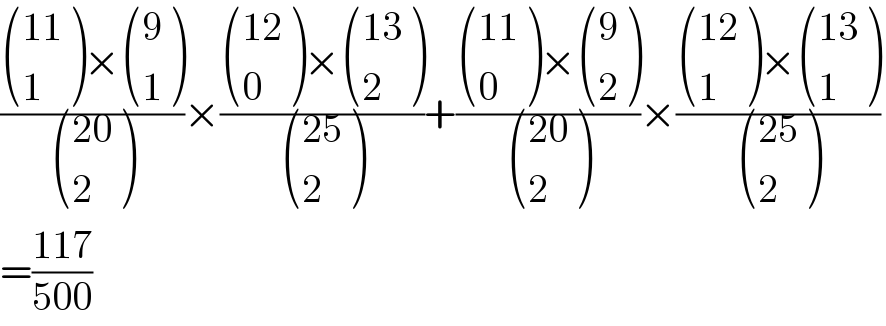
$$\frac{\begin{pmatrix}{\mathrm{11}}\\{\mathrm{1}}\end{pmatrix}×\begin{pmatrix}{\mathrm{9}}\\{\mathrm{1}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{20}}\\{\mathrm{2}}\end{pmatrix}}×\frac{\begin{pmatrix}{\mathrm{12}}\\{\mathrm{0}}\end{pmatrix}×\begin{pmatrix}{\mathrm{13}}\\{\mathrm{2}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{25}}\\{\mathrm{2}}\end{pmatrix}}+\frac{\begin{pmatrix}{\mathrm{11}}\\{\mathrm{0}}\end{pmatrix}×\begin{pmatrix}{\mathrm{9}}\\{\mathrm{2}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{20}}\\{\mathrm{2}}\end{pmatrix}}×\frac{\begin{pmatrix}{\mathrm{12}}\\{\mathrm{1}}\end{pmatrix}×\begin{pmatrix}{\mathrm{13}}\\{\mathrm{1}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{25}}\\{\mathrm{2}}\end{pmatrix}} \\ $$$$=\frac{\mathrm{117}}{\mathrm{500}} \\ $$
Commented by Aina Samuel Temidayo last updated on 02/Sep/20

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{a}\:\mathrm{correct}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{problem}? \\ $$
Answered by john santu last updated on 02/Sep/20

Commented by Aina Samuel Temidayo last updated on 02/Sep/20

$$\mathrm{Yes}.\:\mathrm{Thanks}. \\ $$
