Question Number 104708 by byaw last updated on 23/Jul/20

$$ \\ $$$$\:\mathrm{A}\:\mathrm{bag}\:\mathrm{contains}\:\mathrm{12}\:\mathrm{white}\:\mathrm{balls}\: \\ $$$$\mathrm{and}\:\mathrm{8}\:\mathrm{black}\:\mathrm{balls},\:\mathrm{another}\: \\ $$$$\mathrm{contains}\:\mathrm{10}\:\mathrm{white}\:\mathrm{balls}\:\mathrm{and}\:\mathrm{15} \\ $$$$\mathrm{black}\:\mathrm{balls}.\:\mathrm{If}\:\mathrm{two}\:\mathrm{balls}\:\mathrm{are}\:\mathrm{drawn} \\ $$$$\mathrm{wthout}\:\mathrm{replacement}\:\mathrm{from}\:\mathrm{each} \\ $$$$\mathrm{bag},\:\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}:\: \\ $$$$ \\ $$$$\mathrm{i}.\:\mathrm{all}\:\mathrm{the}\:\mathrm{four}\:\mathrm{balls}\:\mathrm{are}\:\mathrm{black}\: \\ $$$$ \\ $$$$\mathrm{ii}.\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{four}\:\mathrm{balls}\:\mathrm{is} \\ $$$$\mathrm{white} \\ $$
Answered by som(math1967) last updated on 23/Jul/20

$$\left.\mathrm{i}\right)\:\mathrm{All}\:\mathrm{4}\:\mathrm{balls}\:\mathrm{are}\:\mathrm{black} \\ $$$$\frac{\overset{\mathrm{8}} {\mathrm{c}}_{\mathrm{2}} }{\overset{\mathrm{20}} {\mathrm{c}}_{\mathrm{2}} }×\frac{\overset{\mathrm{15}} {\mathrm{c}}_{\mathrm{2}} }{\overset{\mathrm{25}} {\mathrm{c}}_{\mathrm{2}} }=\frac{\mathrm{28}}{\mathrm{190}}×\frac{\mathrm{105}}{\mathrm{300}}=\frac{\mathrm{28}}{\mathrm{950}} \\ $$$$\left.\mathrm{ii}\right)\frac{\overset{\mathrm{8}} {\mathrm{c}}_{\mathrm{2}} }{\overset{\mathrm{20}} {\mathrm{c}}_{\mathrm{2}} }×\frac{\overset{\mathrm{15}} {\mathrm{c}}_{\mathrm{1}} ×\overset{\mathrm{10}} {\mathrm{c}}_{\mathrm{1}} }{\overset{\mathrm{25}} {\mathrm{c}}_{\mathrm{2}} }\:+\frac{\overset{\mathrm{8}} {\mathrm{c}}_{\mathrm{1}} ×\overset{\mathrm{12}} {\mathrm{c}}_{\mathrm{1}} }{\overset{\mathrm{20}} {\mathrm{c}}_{\mathrm{2}} }×\frac{\overset{\mathrm{15}} {\mathrm{c}}_{\mathrm{2}} }{\overset{\mathrm{25}} {\mathrm{c}}_{\mathrm{2}} } \\ $$
Commented by byaw last updated on 23/Jul/20

$${please}\:{help}\:{with}\:{the}\:{question} \\ $$$${below} \\ $$$$ \\ $$$$\:\mathrm{A}\:\mathrm{box}\:\mathrm{contains}\:\mathrm{5}\:\mathrm{white}\:\mathrm{3}\:\mathrm{black} \\ $$$$\mathrm{balls}\:\mathrm{and}\:\mathrm{2}\:\mathrm{red}\:\mathrm{balls}\:\mathrm{of}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{size}.\:\mathrm{A}\:\mathrm{ball}\:\mathrm{is}\:\mathrm{selected}\:\mathrm{at}\:\mathrm{random} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{box}\:\mathrm{and}\:\mathrm{then}\:\mathrm{replaced}.\:\mathrm{A} \\ $$$$\mathrm{second}\:\mathrm{ball}\:\mathrm{is}\:\mathrm{then}\:\mathrm{selected}.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\:\mathrm{obtaining}\:\mathrm{one} \\ $$$$\mathrm{black}\:\mathrm{ball}\:\mathrm{or}\:\mathrm{red}\:\mathrm{ball} \\ $$
Commented by som(math1967) last updated on 24/Jul/20
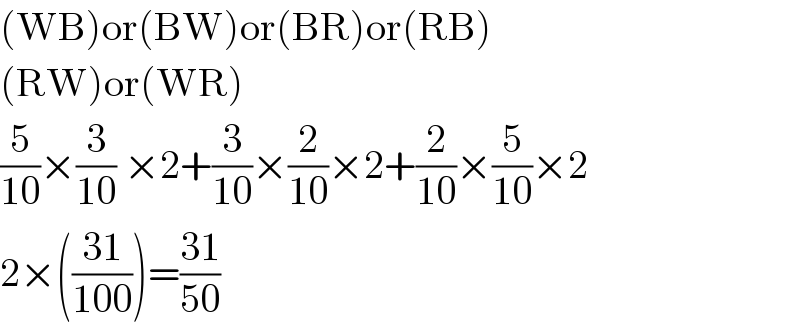
$$\left(\mathrm{WB}\right)\mathrm{or}\left(\mathrm{BW}\right)\mathrm{or}\left(\mathrm{BR}\right)\mathrm{or}\left(\mathrm{RB}\right) \\ $$$$\left(\mathrm{RW}\right)\mathrm{or}\left(\mathrm{WR}\right) \\ $$$$\frac{\mathrm{5}}{\mathrm{10}}×\frac{\mathrm{3}}{\mathrm{10}}\:×\mathrm{2}+\frac{\mathrm{3}}{\mathrm{10}}×\frac{\mathrm{2}}{\mathrm{10}}×\mathrm{2}+\frac{\mathrm{2}}{\mathrm{10}}×\frac{\mathrm{5}}{\mathrm{10}}×\mathrm{2} \\ $$$$\mathrm{2}×\left(\frac{\mathrm{31}}{\mathrm{100}}\right)=\frac{\mathrm{31}}{\mathrm{50}} \\ $$
Commented by 1549442205PVT last updated on 24/Jul/20

$$\mathrm{this}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{for}\:\mathrm{the}\:\mathrm{question}: \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{probality}\:\mathrm{so}\:\mathrm{that} \\ $$$$\mathrm{two}\:\mathrm{balls}\:\mathrm{drawn}\: \\ $$$$\mathrm{different}\:\mathrm{colour}\:\mathrm{sir}?\mathrm{Sir}\:\mathrm{looking}\:\mathrm{back}\:\mathrm{once}\:\mathrm{again}\: \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{of}\:\mathrm{problem}! \\ $$
Commented by som(math1967) last updated on 24/Jul/20
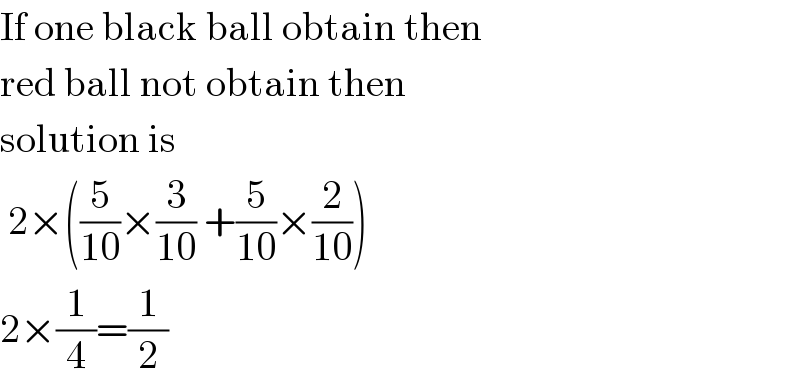
$$\mathrm{If}\:\mathrm{one}\:\mathrm{black}\:\mathrm{ball}\:\mathrm{obtain}\:\mathrm{then} \\ $$$$\mathrm{red}\:\mathrm{ball}\:\mathrm{not}\:\mathrm{obtain}\:\mathrm{then} \\ $$$$\mathrm{solution}\:\mathrm{is} \\ $$$$\:\mathrm{2}×\left(\frac{\mathrm{5}}{\mathrm{10}}×\frac{\mathrm{3}}{\mathrm{10}}\:+\frac{\mathrm{5}}{\mathrm{10}}×\frac{\mathrm{2}}{\mathrm{10}}\right) \\ $$$$\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by byaw last updated on 24/Jul/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
