Question Number 51107 by peter frank last updated on 24/Dec/18

$${A}\:{ball}\:{is}\:{bouncing}\:{down} \\ $$$${a}\:{flight}\:{of}\:{stairs}.{The}\: \\ $$$${coefficiate}\:{of}\:{restitution} \\ $$$${is}\:{e}.{The}\:{height}\:{of}\:{each}\:{step} \\ $$$${d}\:{and}\:{the}\:{ball}\:{descends} \\ $$$${one}\:{step}\:{at}\:{each}\:{bounce}. \\ $$$${After}\:{each}\:{bounce}\:{it}\:{rebounds} \\ $$$${to}\:{heigt}\:\:{h}\:{above}\:{the}\:{next} \\ $$$${lower}\:{step}.{The}\:{height}\:{h}\:{is}/ \\ $$$${large}\:{enough}\:{compare}\:{with} \\ $$$${width}\:{of}\:{a}\:{step}\:{that} \\ $$$${the}\:{empacts}\:{are}\:{effectively}\: \\ $$$${head}\:{on}.{show}\:{that} \\ $$$${h}=\frac{{d}}{\mathrm{1}−{e}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by peter frank last updated on 24/Dec/18

$${sir}\:{we}\:{are}\:{given}\:{that}\:{the}\:{ball}\:{descend} \\ $$$${one}\:{step}\:{at}\:{each}\:{bounce}.{so}\: \\ $$$${ball}\:{falls}\:{a}\:{distance}\:{h}\:{from} \\ $$$${its}\:{heighest}\:\:{position}\:{and}\: \\ $$$${rebounds}\:{to}\:{a}\:{distance} \\ $$$$\left({h}−{d}\right)\:{i}\:{think}. \\ $$
Answered by mr W last updated on 24/Dec/18

$${height}\:{of}\:{the}\:{ball}\:{before}\:{rebound}:\:{h} \\ $$$${height}\:{of}\:{the}\:{ball}\:{after}\:{rebound}:\:{h}−{d} \\ $$$${velocity}\:{of}\:{the}\:{ball}\:{before}\:{rebound}:\:{v}_{{before}} \\ $$$${velocity}\:{of}\:{the}\:{ball}\:{after}\:{rebound}:\:{v}_{{after}} \\ $$$${E}_{{before}} ={mgh}=\frac{\mathrm{1}}{\mathrm{2}}{mv}_{{before}} ^{\mathrm{2}} \\ $$$${E}_{{after}} ={mg}\left({h}−{d}\right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}_{{after}} ^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{h}−{d}}{{h}}=\left(\frac{{v}_{{after}} }{{v}_{{before}} }\right)^{\mathrm{2}} \\ $$$${since}\:{v}_{{after}} ={ev}_{{before}} \\ $$$$\Rightarrow\frac{{h}−{d}}{{h}}={e}^{\mathrm{2}} \\ $$$$\Rightarrow{h}−{d}={e}^{\mathrm{2}} {h} \\ $$$$\Rightarrow{h}=\frac{{d}}{\mathrm{1}−{e}^{\mathrm{2}} } \\ $$
Answered by peter frank last updated on 24/Dec/18
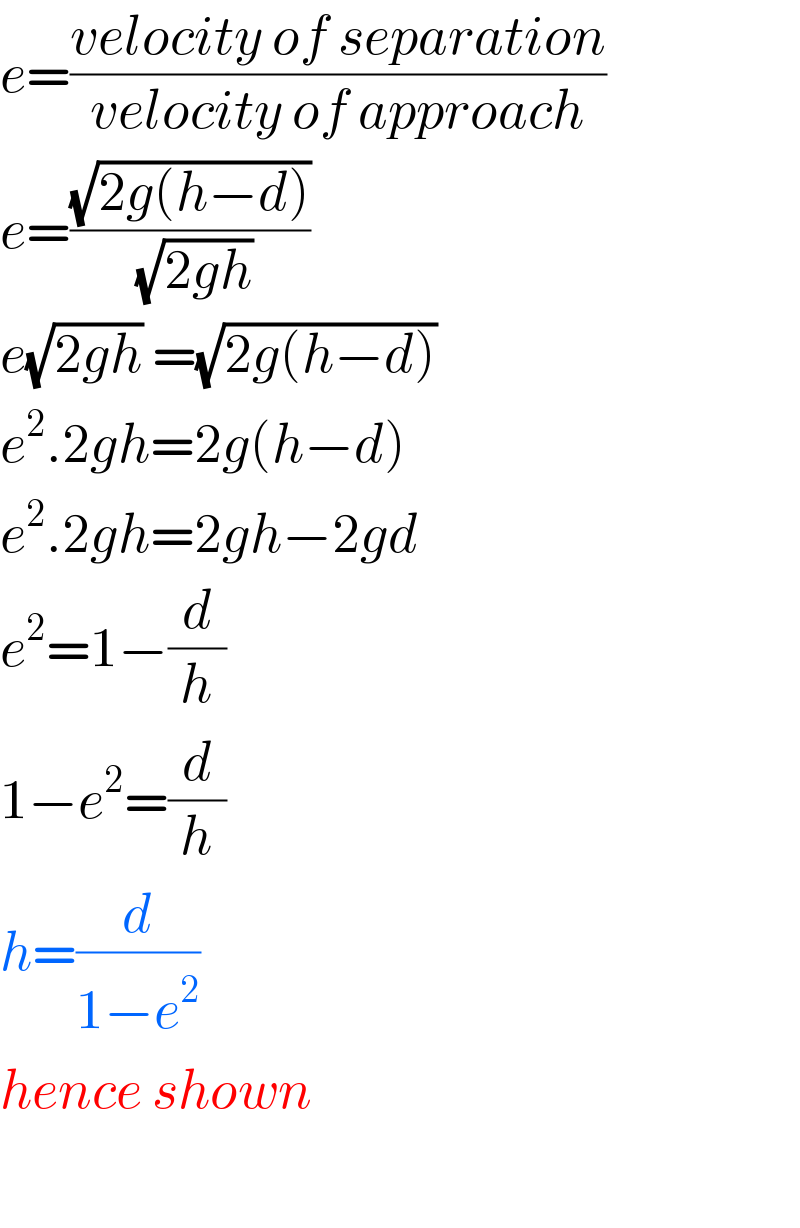
$${e}=\frac{{velocity}\:{of}\:{separation}}{{velocity}\:{of}\:{approach}} \\ $$$${e}=\frac{\sqrt{\mathrm{2}{g}\left({h}−{d}\right)}}{\:\sqrt{\mathrm{2}{gh}}} \\ $$$${e}\sqrt{\mathrm{2}{gh}}\:=\sqrt{\mathrm{2}{g}\left({h}−{d}\right)}\: \\ $$$${e}^{\mathrm{2}} .\mathrm{2}{gh}=\mathrm{2}{g}\left({h}−{d}\right) \\ $$$${e}^{\mathrm{2}} .\mathrm{2}{gh}=\mathrm{2}{gh}−\mathrm{2}{gd} \\ $$$${e}^{\mathrm{2}} =\mathrm{1}−\frac{{d}}{{h}} \\ $$$$\mathrm{1}−{e}^{\mathrm{2}} =\frac{{d}}{{h}} \\ $$$${h}=\frac{{d}}{\mathrm{1}−{e}^{\mathrm{2}} } \\ $$$${hence}\:{shown} \\ $$$$ \\ $$
Commented by mr W last updated on 24/Dec/18
$${sorry},\:{i}\:{misread}\:{the}\:{information}\:{about}\:{h}. \\ $$$${now}\:{it}'{s}\:{fixed}. \\ $$
Commented by peter frank last updated on 24/Dec/18

$${okay}\:{sir}. \\ $$
