Menu Close

A-ball-is-dropped-vertically-from-a-height-d-above-the-ground-It-hits-the-ground-and-bounces-up-vertically-to-a-height-d-2-Neglecting-subsequent-motion-and-air-resistance-its-velocity-V-varies-wit

Tinku Tara 0 Comments
Pin




Question Number 16647 by Tinkutara last updated on 24/Jun/17
A ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a height (d/2). Neglecting subsequent motion and air resistance its velocity V varies with height h above the ground is
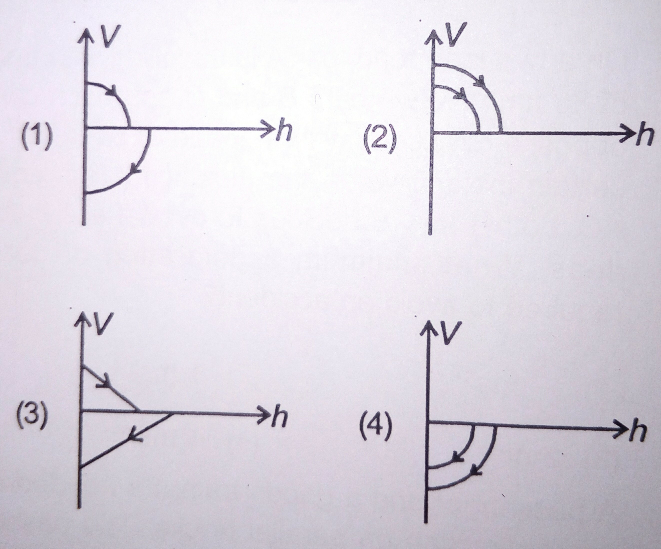
$$\mathrm{A}\:\mathrm{ball}\:\mathrm{is}\:\mathrm{dropped}\:\mathrm{vertically}\:\mathrm{from}\:\mathrm{a} \\ $$$$\mathrm{height}\:{d}\:\mathrm{above}\:\mathrm{the}\:\mathrm{ground}.\:\mathrm{It}\:\mathrm{hits}\:\mathrm{the} \\ $$$$\mathrm{ground}\:\mathrm{and}\:\mathrm{bounces}\:\mathrm{up}\:\mathrm{vertically}\:\mathrm{to}\:\mathrm{a} \\ $$$$\mathrm{height}\:\frac{{d}}{\mathrm{2}}.\:\mathrm{Neglecting}\:\mathrm{subsequent} \\ $$$$\mathrm{motion}\:\mathrm{and}\:\mathrm{air}\:\mathrm{resistance}\:\mathrm{its}\:\mathrm{velocity} \\ $$$${V}\:\mathrm{varies}\:\mathrm{with}\:\mathrm{height}\:{h}\:\mathrm{above}\:\mathrm{the} \\ $$$$\mathrm{ground}\:\mathrm{is} \\ $$
Commented by Tinkutara last updated on 24/Jun/17
Commented by ajfour last updated on 02/Jul/17
ball falls, initially height is +ve (H_0 ), as h decreases v , from zero becomes more and more −ve, as h=0 v from max. −ve at once becomes +ve (slightly less +ve than its max.−ve, owing to e<1) as h increases v decreases becomes zero and decreases again till h→0 and gets +ve due to impulse as it hits the ground. if h=height above ground and H_0 the initial height H_1 : max. height after 1^(st) bounce,.. v=±(√(2g(H_i −h))) if i≠0 =−(√(2g(H_0 −h))) for i=0 . correct option is (1).
$$\mathrm{ball}\:\mathrm{falls},\:\mathrm{initially}\:\mathrm{height}\:\mathrm{is}\:+\mathrm{ve}\:\left(\mathrm{H}_{\mathrm{0}} \right), \\ $$$$\mathrm{as}\:\mathrm{h}\:\mathrm{decreases}\:\mathrm{v}\:,\:\mathrm{from}\:\mathrm{zero}\:\mathrm{becomes} \\ $$$$\mathrm{more}\:\mathrm{and}\:\mathrm{more}\:−\mathrm{ve},\:\mathrm{as}\:\mathrm{h}=\mathrm{0}\: \\ $$$$\mathrm{v}\:\mathrm{from}\:\mathrm{max}.\:−\mathrm{ve}\:\mathrm{at}\:\mathrm{once}\:\mathrm{becomes} \\ $$$$+\mathrm{ve}\:\left(\mathrm{slightly}\:\mathrm{less}\:+\mathrm{ve}\:\mathrm{than}\:\mathrm{its}\right. \\ $$$$\left.\mathrm{max}.−\mathrm{ve},\:\mathrm{owing}\:\mathrm{to}\:\mathrm{e}<\mathrm{1}\right)\:\mathrm{as}\: \\ $$$$\mathrm{h}\:\mathrm{increases}\:\mathrm{v}\:\mathrm{decreases}\:\mathrm{becomes} \\ $$$$\mathrm{zero}\:\mathrm{and}\:\mathrm{decreases}\:\mathrm{again}\:\mathrm{till} \\ $$$$\mathrm{h}\rightarrow\mathrm{0}\:\mathrm{and}\:\mathrm{gets}\:+\mathrm{ve}\:\mathrm{due}\:\mathrm{to}\:\mathrm{impulse} \\ $$$$\mathrm{as}\:\mathrm{it}\:\mathrm{hits}\:\mathrm{the}\:\mathrm{ground}. \\ $$$$\mathrm{if}\:\mathrm{h}=\mathrm{height}\:\mathrm{above}\:\mathrm{ground} \\ $$$$\mathrm{and}\:\:\mathrm{H}_{\mathrm{0}} \:\mathrm{the}\:\mathrm{initial}\:\mathrm{height} \\ $$$$\mathrm{H}_{\mathrm{1}} :\:\mathrm{max}.\:\mathrm{height}\:\mathrm{after}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{bounce},.. \\ $$$$\mathrm{v}=\pm\sqrt{\mathrm{2g}\left(\mathrm{H}_{\boldsymbol{\mathrm{i}}} −\mathrm{h}\right)}\:\mathrm{if}\:\mathrm{i}\neq\mathrm{0} \\ $$$$\:\:=−\sqrt{\mathrm{2g}\left(\mathrm{H}_{\mathrm{0}} −\mathrm{h}\right)}\:\:\mathrm{for}\:\:\mathrm{i}=\mathrm{0}\:. \\ $$$$\mathrm{correct}\:\mathrm{option}\:\mathrm{is}\:\left(\mathrm{1}\right). \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17
Answer (1) is correct.
$$\mathrm{Answer}\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{correct}. \\ $$
Commented by Tinkutara last updated on 02/Jul/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *