A-biology-class-at-central-high-school-predicted-that-a-local-population-of-animals-will-double-in-size-every-12-years-The-population-at-the-beginning-of-2014-was-estimated-to

Question Number 175280 by naka3546 last updated on 26/Aug/22

$$\mathrm{A}\:\mathrm{biology}\:\:\mathrm{class}\:\mathrm{at}\:\mathrm{central}\:\:\mathrm{high}\:\:\mathrm{school} \\ $$$$\mathrm{predicted}\:\:\mathrm{that}\:\:\mathrm{a}\:\:\mathrm{local}\:\:\mathrm{population}\:\:\mathrm{of}\:\:\:\mathrm{animals} \\ $$$$\mathrm{will}\:\:\mathrm{double}\:\:\mathrm{in}\:\:\mathrm{size}\:\:\mathrm{every}\:\:\mathrm{12}\:\:\mathrm{years}. \\ $$$$\mathrm{The}\:\:\mathrm{population}\:\:\mathrm{at}\:\:\mathrm{the}\:\:\mathrm{beginning}\:\:\mathrm{of}\:\:\mathrm{2014} \\ $$$$\mathrm{was}\:\:\mathrm{estimated}\:\:\mathrm{to}\:\mathrm{be}\:\:\mathrm{50}\:\:\mathrm{animals}. \\ $$$$\mathrm{If}\:\:{P}\:\:\mathrm{represents}\:\:\mathrm{the}\:\:\mathrm{population}\:\:{n}\:\:\mathrm{years}\:\:\mathrm{after}\:\:\mathrm{2014}. \\ $$$$\mathrm{Find}\:\:\mathrm{the}\:\:\mathrm{equations}\:\:\mathrm{represents}\:\:\mathrm{the}\:\:\mathrm{class}\:\:\mathrm{model} \\ $$$$\mathrm{of}\:\:\mathrm{the}\:\:\mathrm{population}\:\:\mathrm{over}\:\:\mathrm{time}? \\ $$

Answered by MJS_new last updated on 26/Aug/22

$${P}=\mathrm{50}×\mathrm{2}^{{n}/\mathrm{12}} \\ $$

Answered by FelipeLz last updated on 26/Aug/22

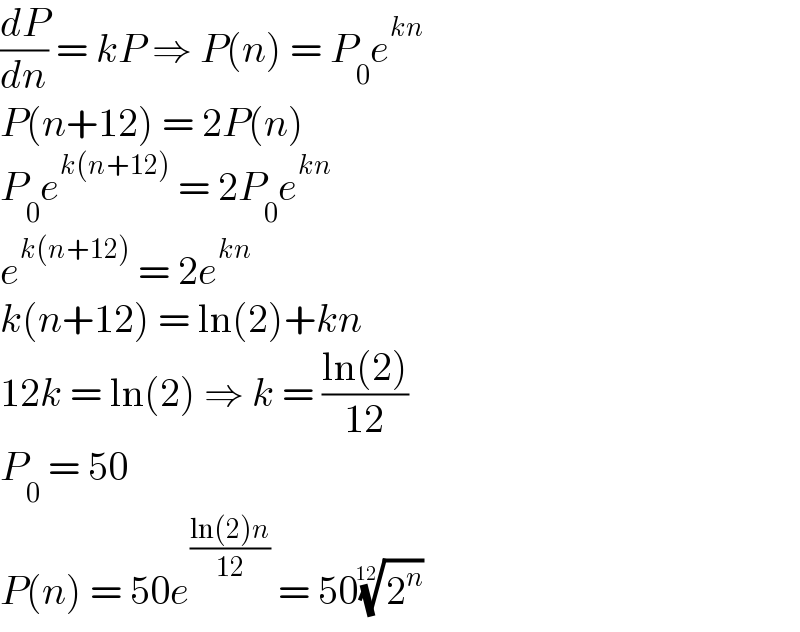
(dP/dn) = kP ⇒ P(n) = P_0 e^(kn) P(n+12) = 2P(n) P_0 e^(k(n+12)) = 2P_0 e^(kn) e^(k(n+12)) = 2e^(kn) k(n+12) = ln(2)+kn 12k = ln(2) ⇒ k = ((ln(2))/(12)) P_0 = 50 P(n) = 50e^((ln(2)n)/(12)) = 50(2^n )^(1/(12))

$$\frac{{dP}}{{dn}}\:=\:{kP}\:\Rightarrow\:{P}\left({n}\right)\:=\:{P}_{\mathrm{0}} {e}^{{kn}} \\ $$$${P}\left({n}+\mathrm{12}\right)\:=\:\mathrm{2}{P}\left({n}\right) \\ $$$${P}_{\mathrm{0}} {e}^{{k}\left({n}+\mathrm{12}\right)} \:=\:\mathrm{2}{P}_{\mathrm{0}} {e}^{{kn}} \\ $$$${e}^{{k}\left({n}+\mathrm{12}\right)} \:=\:\mathrm{2}{e}^{{kn}} \\ $$$${k}\left({n}+\mathrm{12}\right)\:=\:\mathrm{ln}\left(\mathrm{2}\right)+{kn} \\ $$$$\mathrm{12}{k}\:=\:\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\:{k}\:=\:\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{12}} \\ $$$${P}_{\mathrm{0}} \:=\:\mathrm{50} \\ $$$${P}\left({n}\right)\:=\:\mathrm{50}{e}^{\frac{\mathrm{ln}\left(\mathrm{2}\right){n}}{\mathrm{12}}} \:=\:\mathrm{50}\sqrt[{\mathrm{12}}]{\mathrm{2}^{{n}} } \\ $$

Commented by MJS_new last updated on 26/Aug/22