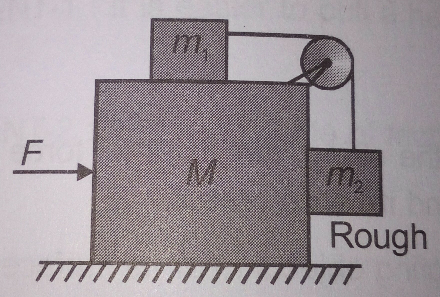
A-block-of-mass-M-is-placed-on-smooth-ground-Its-upper-surface-is-smooth-and-vertical-surface-is-rough-with-coefficient-of-friction-A-block-of-mass-m-1-is-placed-on-its-horizontal-surface-and-tie
Question Number 21564 by Tinkutara last updated on 27/Sep/17
Commented by Tinkutara last updated on 27/Sep/17