A-body-is-released-from-rest-at-the-top-ofa-plane-inclined-at-30-to-the-horizontaland-4-0m-high-If-the-coefficiet-of-friction-between-the-body-and-plane-is-0-3-calculate-to-the-time-theb-ody-take

FacebookTweetPin

Question Number 120365 by help last updated on 30/Oct/20

$$\mathrm{A}\mathrm{body}\mathrm{is}\mathrm{released}\mathrm{from}\mathrm{rest}\mathrm{at}\mathrm{the}\mathrm{top}$$$$\mathrm{ofa}\mathrm{plane}\mathrm{inclined}\mathrm{at}30\mathrm{to}\mathrm{the}$$$$\mathrm{horizontaland}4.0\mathrm{m}\mathrm{high}.\mathrm{If}\mathrm{the}$$$$\mathrm{coefficiet}\mathrm{of}\mathrm{friction}\mathrm{between}\mathrm{the}\mathrm{body}$$$$\mathrm{an}d\mathrm{plane}\mathrm{is}0.3.\mathrm{calculate}\mathrm{to}\mathrm{the}\mathrm{time}\mathrm{theb}$$$$\mathrm{ody}\mathrm{takes}\mathrm{to}\mathrm{reach}\mathrm{the}\mathrm{bottom}\mathrm{of}.\mathrm{thea}$$

Commented by Dwaipayan Shikari last updated on 30/Oct/20

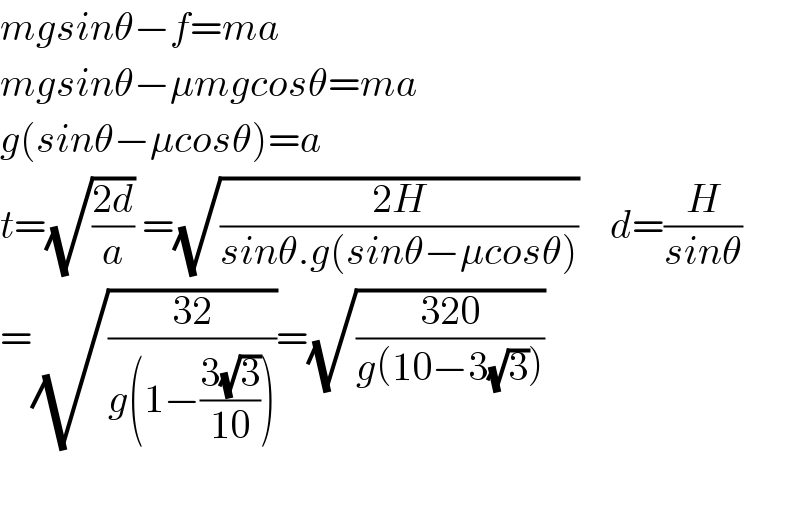
$$mgsin\theta -f=ma$$$$mgsin\theta -\mu mgcos\theta =ma$$$$g(sin\theta -\mu cos\theta )=a$$$$t=\sqrt{\frac{2d}{a}}=\sqrt{\frac{2H}{sin\theta .g(sin\theta -\mu cos\theta )}}d=\frac{H}{sin\theta }$$$$=\sqrt{\frac{32}{g(1-\frac{3\sqrt{3}}{10})}}=\sqrt{\frac{320}{g(10-3\sqrt{3})}}$$$$$$

Commented by peter frank last updated on 31/Oct/20

$$\mathrm{diagram}\mathrm{please}$$

Commented by Dwaipayan Shikari last updated on 31/Oct/20

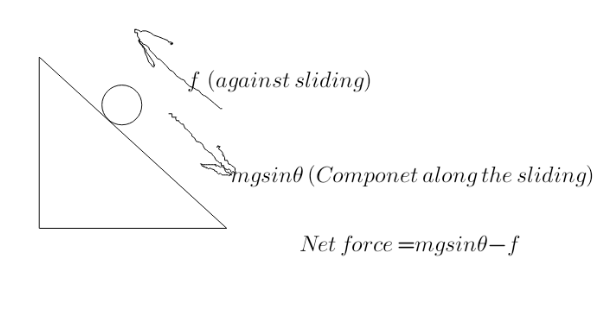
Commented by peter frank last updated on 31/Oct/20

$$\mathrm{thank}\mathrm{you}$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin