A-body-resting-on-a-rough-horizontal-plane-require-a-pull-of-18N-inclined-at-30-to-the-plane-first-to-move-it-It-was-found-that-a-push-of-22N-inclined-at-30-to-the-plane-just-moved-the-body-Determi

Question Number 27128 by NECx last updated on 02/Jan/18

A b o d y r e s t i n g o n a r o u g h

h o r i z o n t a l p l a n e r e q u i r e a p u l l o f

18 N i n c l i n e d a t 30 ° t o t h e p l a n e

f i r s t t o m o v e i t . I t w a s f o u n d

t h a t a p u s h o f 22 N i n c l i n e d a t 30 °

t o t h e p l a n e j u s t m o v e d t h e b o d y .

D e t e r m i n e t h e w e i g h t a n d

c o e f f i c i e n t o f f r i c t i o n .

Answered by mrW1 last updated on 02/Jan/18

P u l l : F_{1} \cos α_{1} = μ (m g - F_{1} \sin α_{1}) \dots (i)

P u s h : F_{2} \cos α_{2} = μ (m g + F_{2} \sin α_{2}) \dots (i i)

(i) / (i i) :

\Rightarrow \frac{F_{1} \cos α_{1}}{F_{2} \cos α_{2}} = \frac{m g - F_{1} \sin α_{1}}{m g + F_{2} \sin α_{2}}

\Rightarrow \frac{F_{1} \cos α_{1}}{F_{2} \cos α_{2}} = \frac{m g + F_{2} \sin α_{2} - F_{1} \sin α_{1} - F_{2} \sin α_{2}}{m g + F_{2} \sin α_{2}}

\Rightarrow \frac{F_{1} \cos α_{1}}{F_{2} \cos α_{2}} = 1 - \frac{F_{1} \sin α_{1} + F_{2} \sin α_{2}}{m g + F_{2} \sin α_{2}}

\Rightarrow 1 - \frac{F_{1} \cos α_{1}}{F_{2} \cos α_{2}} = \frac{F_{1} \sin α_{1} + F_{2} \sin α_{2}}{m g + F_{2} \sin α_{2}}

\Rightarrow m g = \frac{F_{1} \sin α_{1} + F_{2} \sin α_{2}}{1 - \frac{F_{1} \cos α_{1}}{F_{2} \cos α_{2}}} - F_{2} \sin α_{2}

\Rightarrow m g = F_{2} \sin α_{2} (\frac{1 + \frac{F_{1} \sin α_{1}}{F_{2} \sin α_{2}}}{1 - \frac{F_{1} \cos α_{1}}{F_{2} \cos α_{2}}} - 1)

α_{1} = α_{2} = 30 °

\Rightarrow m g = 22 \times \frac{1}{2} (\frac{1 + \frac{18}{22}}{1 - \frac{18}{22}} - 1) = 11 \times 9 = 99 N

(i i) - (i) :

F_{2} \cos α_{2} - F_{1} \cos α_{1} = μ (F_{2} \sin α_{2} + F_{1} \sin α_{1})

\Rightarrow μ = \frac{F_{2} \cos α_{2} - F_{1} \cos α_{1}}{F_{2} \sin α_{2} + F_{1} \sin α_{1}}

\Rightarrow μ = \frac{22 - 18}{22 + 18} \times \frac{\cos 30 °}{\sin 30 °} = \frac{\sqrt{3}}{10} = 0.173

Commented by NECx last updated on 02/Jan/18

p l e a s e c a n y o u p o s t a d i a g r a m f o r

b e t t e r u n d e r s t a n d i n g . T h i s i s

b e c a u s e I n e v e r k n e w t h a t t h e r e

w a s a d i f f e r e n c e b e t w e e n t h e r e a c t i o n

o f f o r c e s w h e n i n a p u s h a n d p u l l .

Commented by mrW1 last updated on 02/Jan/18

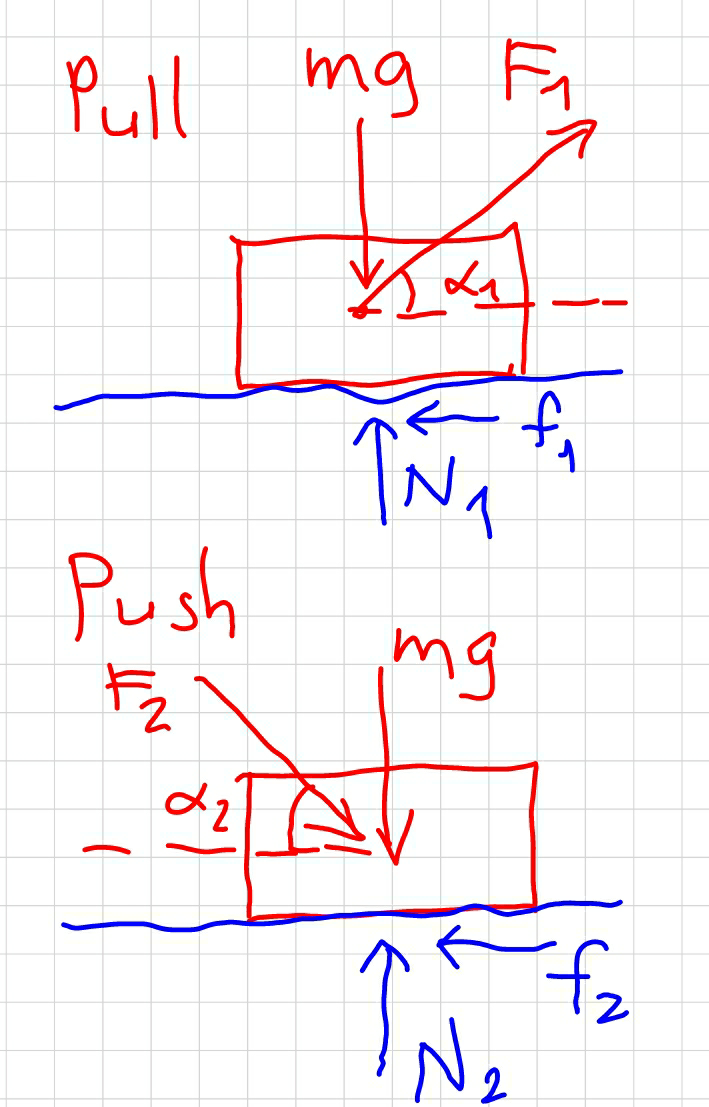
Commented by NECx last updated on 02/Jan/18

p l e a s e t h e d i a g r a m y o u d i s p l a y e d

i s n o t s h o w i n g p l e a s e c a n y o u p o s t

i t a s a q u e s t i o n .

Facebook Tweet Pin