Question Number 128103 by byaw last updated on 04/Jan/21

$$ \\ $$$$\mathrm{A}\:\mathrm{box}\:\mathrm{contains}\:\mathrm{4}\:\mathrm{black}\:\mathrm{5}\:\mathrm{white} \\ $$$$\mathrm{and}\:\mathrm{6}\:\mathrm{red}\:\mathrm{shirts}.\:\mathrm{3}\:\mathrm{are}\:\mathrm{drawn}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{box}\:\mathrm{one}\:\mathrm{after}\:\mathrm{the}\:\mathrm{other}\: \\ $$$$\mathrm{without}\:\mathrm{replacement}.\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{proability}\:\mathrm{that}\:\mathrm{two}\:\mathrm{of}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{color}\:\mathrm{and}\:\mathrm{one}\:\mathrm{a}\:\mathrm{different}\:\mathrm{color}. \\ $$
Answered by liberty last updated on 04/Jan/21
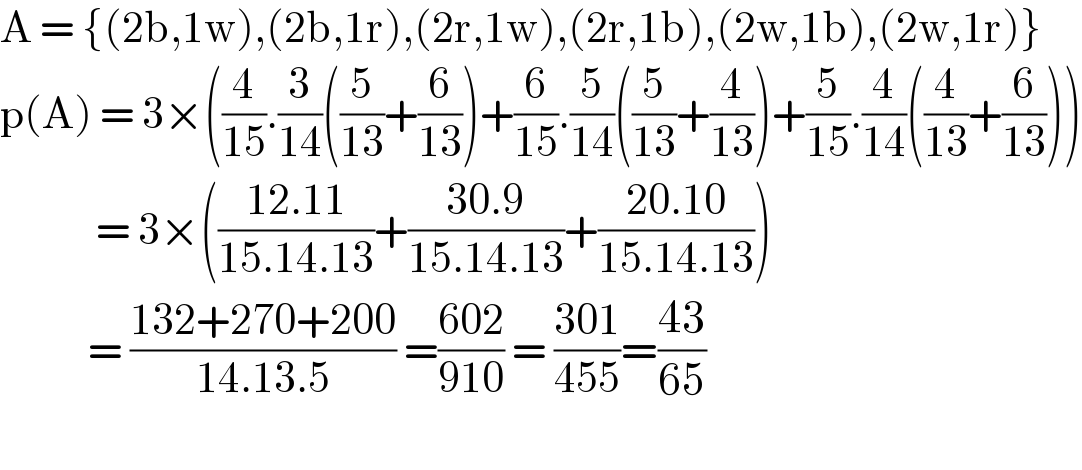
$$\mathrm{A}\:=\:\left\{\left(\mathrm{2b},\mathrm{1w}\right),\left(\mathrm{2b},\mathrm{1r}\right),\left(\mathrm{2r},\mathrm{1w}\right),\left(\mathrm{2r},\mathrm{1b}\right),\left(\mathrm{2w},\mathrm{1b}\right),\left(\mathrm{2w},\mathrm{1r}\right)\right\} \\ $$$$\mathrm{p}\left(\mathrm{A}\right)\:=\:\mathrm{3}×\left(\frac{\mathrm{4}}{\mathrm{15}}.\frac{\mathrm{3}}{\mathrm{14}}\left(\frac{\mathrm{5}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{13}}\right)+\frac{\mathrm{6}}{\mathrm{15}}.\frac{\mathrm{5}}{\mathrm{14}}\left(\frac{\mathrm{5}}{\mathrm{13}}+\frac{\mathrm{4}}{\mathrm{13}}\right)+\frac{\mathrm{5}}{\mathrm{15}}.\frac{\mathrm{4}}{\mathrm{14}}\left(\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{13}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3}×\left(\frac{\mathrm{12}.\mathrm{11}}{\mathrm{15}.\mathrm{14}.\mathrm{13}}+\frac{\mathrm{30}.\mathrm{9}}{\mathrm{15}.\mathrm{14}.\mathrm{13}}+\frac{\mathrm{20}.\mathrm{10}}{\mathrm{15}.\mathrm{14}.\mathrm{13}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{132}+\mathrm{270}+\mathrm{200}}{\mathrm{14}.\mathrm{13}.\mathrm{5}}\:=\frac{\mathrm{602}}{\mathrm{910}}\:=\:\frac{\mathrm{301}}{\mathrm{455}}=\frac{\mathrm{43}}{\mathrm{65}} \\ $$$$ \\ $$
