A-boy-can-swim-with-a-speed-of-26m-s-in-still-water-He-wants-to-swim-across-a-150m-river-from-a-point-A-to-point-B-which-is-directly-opposite-the-other-side-of-the-river-The-river-flows-with-a-speed-

Question Number 30738 by NECx last updated on 25/Feb/18

A b o y c a n s w i m w i t h a s p e e d o f

26 m / s i n s t i l l w a t e r . H e w a n t s t o

s w i m a c r o s s a 150 m r i v e r f r o m

a p o i n t A t o p o i n t B w h i c h i s

d i r e c t l y o p p o s i t e t h e o t h e r s i d e

o f t h e r i v e r . T h e r i v e r f l o w s w i t h

a s p e e d o f 10 m / s .

i) i f h e a l w a y s s w i m i n t h e

d i r e c t i o n p a r a l l e l t o A B, f i n d h o w

f a r h e l a n d s d o w n s t r e a m o f B .

i i) I n w h a t d i r e c t i o n r e l a t i v e t o

t h e b a n k m u s t h e s w i m s o a s t o

c r o s s d i r e c t l y f r o m A t o B .

Commented by NECx last updated on 25/Feb/18

p l e a s e h e l p

Answered by mrW2 last updated on 26/Feb/18

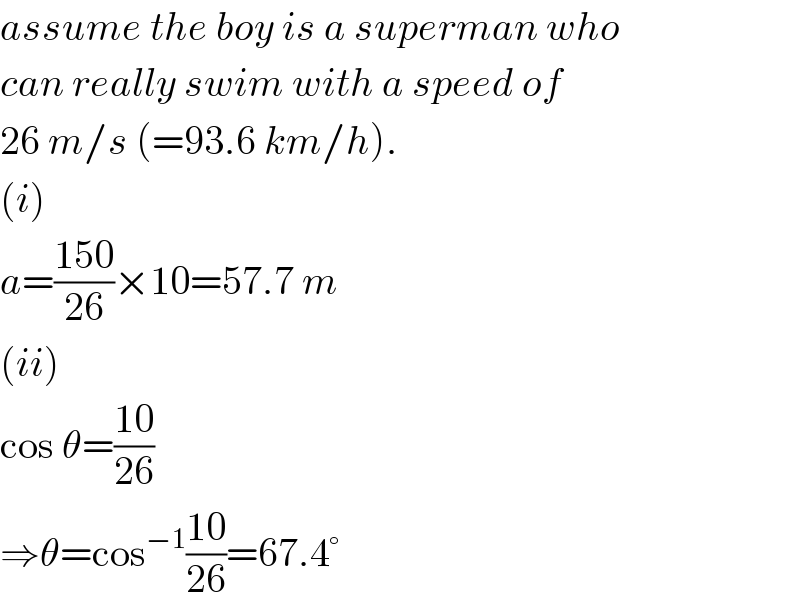
a s s u m e t h e b o y i s a s u p e r m a n w h o

c a n r e a l l y s w i m w i t h a s p e e d o f

26 m / s (= 93.6 k m / h) .

(i)

a = \frac{150}{26} \times 10 = 57.7 m

(i i)

\cos θ = \frac{10}{26}

\Rightarrow θ = \cos^{- 1} \frac{10}{26} = 67.4 °

Facebook Tweet Pin