Menu Close

A-boy-travelling-in-an-open-car-moving-on-a-levelled-road-with-constant-speed-tosses-a-ball-vertically-up-in-the-air-and-catches-it-back-Sketch-the-motion-of-the-ball-as-observed-by-a-boy-standing-on

Tinku Tara 0 Comments
Pin




Question Number 18095 by Tinkutara last updated on 15/Jul/17
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
$$\mathrm{A}\:\mathrm{boy}\:\mathrm{travelling}\:\mathrm{in}\:\mathrm{an}\:\mathrm{open}\:\mathrm{car}\:\mathrm{moving} \\ $$$$\mathrm{on}\:\mathrm{a}\:\mathrm{levelled}\:\mathrm{road}\:\mathrm{with}\:\mathrm{constant}\:\mathrm{speed} \\ $$$$\mathrm{tosses}\:\mathrm{a}\:\mathrm{ball}\:\mathrm{vertically}\:\mathrm{up}\:\mathrm{in}\:\mathrm{the}\:\mathrm{air}\:\mathrm{and} \\ $$$$\mathrm{catches}\:\mathrm{it}\:\mathrm{back}.\:\mathrm{Sketch}\:\mathrm{the}\:\mathrm{motion}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{ball}\:\mathrm{as}\:\mathrm{observed}\:\mathrm{by}\:\mathrm{a}\:\mathrm{boy}\:\mathrm{standing} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{footpath}.\:\mathrm{Give}\:\mathrm{explanation}\:\mathrm{to} \\ $$$$\mathrm{support}\:\mathrm{your}\:\mathrm{diagram}. \\ $$
Answered by Arnab Maiti last updated on 15/Jul/17
Commented by Arnab Maiti last updated on 17/Jul/17
What do you want to know ?
$$\mathrm{What}\:\mathrm{do}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:? \\ $$
Commented by Arnab Maiti last updated on 17/Jul/17
A point to be noted. Here I made a little mistake. I only explain the locus of the ball when it is dropped from h height. The explaination will be same as the locus of a projectile.
$$\mathrm{A}\:\mathrm{point}\:\mathrm{to}\:\mathrm{be}\:\mathrm{noted}.\:\mathrm{Here}\:\mathrm{I}\:\mathrm{made} \\ $$$$\mathrm{a}\:\mathrm{little}\:\mathrm{mistake}.\:\mathrm{I}\:\mathrm{only}\:\mathrm{explain} \\ $$$$\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{when}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{dropped}\:\mathrm{from}\:\mathrm{h}\:\mathrm{height}.\:\mathrm{The}\:\mathrm{explaination} \\ $$$$\mathrm{will}\:\mathrm{be}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{projectile}. \\ $$
Commented by Arnab Maiti last updated on 15/Jul/17
In train the ball has u velocity upwords. It has no horizontal component. But the train is moving with a constant velocity in perpendicular to the motion of the ball (i.e horizontal). Let the time to attend maximum height (h) =t . ∴ h=(1/2)gt^2 ∙∙∙∙∙∙∙∙(1) In that interval the train overcome s distance. Hence, s=vt or, t=(s/v) Now from the (1) we get, ∴ h=(1/2)g×((s/v))^2 ∴ h ∝ s^2 This is a parabolic eqe^n the diagram of h(height) vs s (displacement) is parabolic as shown in the figure.
$$\mathrm{In}\:\mathrm{train}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{has}\:\mathrm{u}\:\mathrm{velocity} \\ $$$$\mathrm{upwords}.\:\mathrm{It}\:\mathrm{has}\:\mathrm{no}\:\mathrm{horizontal} \\ $$$$\mathrm{component}.\:\mathrm{But}\:\mathrm{the}\:\mathrm{train}\:\mathrm{is}\:\mathrm{moving} \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{velocity}\:\mathrm{in} \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{the}\:\mathrm{motion}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{ball}\:\left(\mathrm{i}.\mathrm{e}\:\mathrm{horizontal}\right).\:\mathrm{Let}\:\mathrm{the} \\ $$$$\mathrm{time}\:\mathrm{to}\:\mathrm{attend}\:\mathrm{maximum}\:\mathrm{height} \\ $$$$\left(\mathrm{h}\right)\:=\mathrm{t}\:.\: \\ $$$$\therefore\:\mathrm{h}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} \:\:\:\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\left(\mathrm{1}\right) \\ $$$$\mathrm{In}\:\mathrm{that}\:\mathrm{interval}\:\mathrm{the}\:\mathrm{train}\:\mathrm{overcome} \\ $$$$\mathrm{s}\:\:\mathrm{distance}.\:\mathrm{Hence},\:\mathrm{s}=\mathrm{vt} \\ $$$$\mathrm{or},\:\mathrm{t}=\frac{\mathrm{s}}{\mathrm{v}} \\ $$$$\mathrm{Now}\:\mathrm{from}\:\mathrm{the}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get}, \\ $$$$\therefore\:\mathrm{h}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{g}×\left(\frac{\mathrm{s}}{\mathrm{v}}\right)^{\mathrm{2}} \\ $$$$\therefore\:\mathrm{h}\:\propto\:\mathrm{s}^{\mathrm{2}} \:\:\:\:\:{This}\:{is}\:{a}\:{parabolic}\:{eqe}^{{n}} \\ $$$$\mathrm{the}\:\mathrm{diagram}\:\mathrm{of}\:\:\mathrm{h}\left(\mathrm{height}\right)\:\mathrm{vs}\:\mathrm{s} \\ $$$$\left(\mathrm{displacement}\right)\:\mathrm{is}\:\mathrm{parabolic} \\ $$$$\mathrm{as}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{the}\:\mathrm{figure}. \\ $$
Commented by Tinkutara last updated on 15/Jul/17
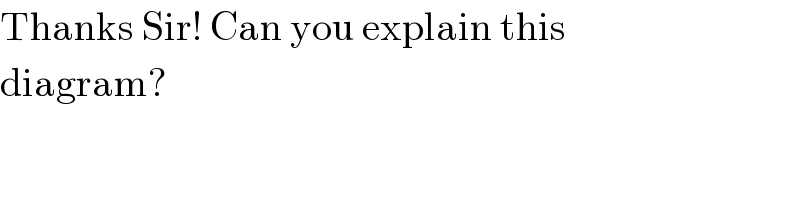
Thanks Sir! Can you explain this diagram?
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{this} \\ $$$$\mathrm{diagram}? \\ $$
Commented by Tinkutara last updated on 15/Jul/17
Commented by Tinkutara last updated on 17/Jul/17
I want to know that why speed of coin tossed increases linearly with the car speed?
$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{that}\:\mathrm{why}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{coin} \\ $$$$\mathrm{tossed}\:\mathrm{increases}\:\mathrm{linearly}\:\mathrm{with}\:\mathrm{the}\:\mathrm{car} \\ $$$$\mathrm{speed}? \\ $$
Commented by Arnab Maiti last updated on 17/Jul/17
The coin is tossed vertically upward with an initial velocity. The diagram speaks the car has an acceleration. But is it constant or increasing constantly? u_1 is the speed where frame of referance is earth. But what is the frame of referance of velocity v ?
$$\mathrm{The}\:\mathrm{coin}\:\mathrm{is}\:\mathrm{tossed}\:\mathrm{vertically}\: \\ $$$$\mathrm{upward}\:\mathrm{with}\:\mathrm{an}\:\mathrm{initial}\:\mathrm{velocity}. \\ $$$$\mathrm{The}\:\mathrm{diagram}\:\mathrm{speaks}\:\mathrm{the}\:\mathrm{car} \\ $$$$\mathrm{has}\:\mathrm{an}\:\mathrm{acceleration}.\:\mathrm{But}\:\mathrm{is}\:\mathrm{it}\: \\ $$$$\mathrm{constant}\:\mathrm{or}\:\mathrm{increasing}\:\mathrm{constantly}? \\ $$$$\mathrm{u}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{where}\:\mathrm{frame}\:\mathrm{of} \\ $$$$\mathrm{referance}\:\mathrm{is}\:\mathrm{earth}.\:\mathrm{But}\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{frame}\:\mathrm{of}\:\mathrm{referance}\:\mathrm{of}\:\mathrm{velocity} \\ $$$$\mathrm{v}\:? \\ $$
Commented by Tinkutara last updated on 17/Jul/17
I now understand that it is the vector sum of u_1 and u_2 , not the variation of u_2 with respect to u_1 . Thanks Sir!
$$\mathrm{I}\:\mathrm{now}\:\mathrm{understand}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{the}\:\mathrm{vector} \\ $$$$\mathrm{sum}\:\mathrm{of}\:{u}_{\mathrm{1}} \:\mathrm{and}\:{u}_{\mathrm{2}} ,\:\mathrm{not}\:\mathrm{the}\:\mathrm{variation}\:\mathrm{of} \\ $$$${u}_{\mathrm{2}} \:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:{u}_{\mathrm{1}} .\:\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *