Question Number 102076 by pete last updated on 06/Jul/20
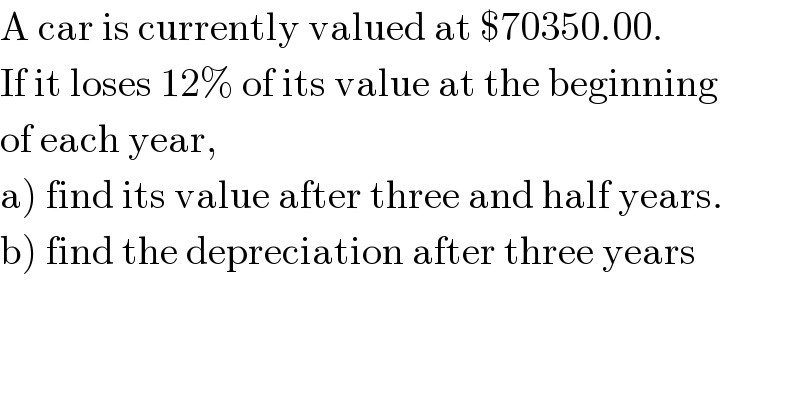
$$\mathrm{A}\:\mathrm{car}\:\mathrm{is}\:\mathrm{currently}\:\mathrm{valued}\:\mathrm{at}\:\$\mathrm{70350}.\mathrm{00}. \\ $$$$\mathrm{If}\:\mathrm{it}\:\mathrm{loses}\:\mathrm{12\%}\:\mathrm{of}\:\mathrm{its}\:\mathrm{value}\:\mathrm{at}\:\mathrm{the}\:\mathrm{beginning} \\ $$$$\mathrm{of}\:\mathrm{each}\:\mathrm{year}, \\ $$$$\left.\mathrm{a}\right)\:\mathrm{find}\:\mathrm{its}\:\mathrm{value}\:\mathrm{after}\:\mathrm{three}\:\mathrm{and}\:\mathrm{half}\:\mathrm{years}. \\ $$$$\left.\mathrm{b}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{depreciation}\:\mathrm{after}\:\mathrm{three}\:\mathrm{years} \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jul/20

$$\mathrm{use}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{C}=\mathrm{current}\:\mathrm{value}\:\mathrm{P}=\:\mathrm{previous}\:\mathrm{value}\: \\ $$$$\mathrm{d}=\mathrm{rate}\:\mathrm{of}\:\mathrm{depriciation}\:\mathrm{t}=\mathrm{time} \\ $$$$\mathrm{then} \\ $$$$\boldsymbol{\mathrm{C}}=\boldsymbol{\mathrm{P}}\left(\mathrm{1}−\frac{\boldsymbol{\mathrm{d}}}{\mathrm{100}}\right)^{\boldsymbol{\mathrm{t}}} \\ $$
Commented by pete last updated on 06/Jul/20
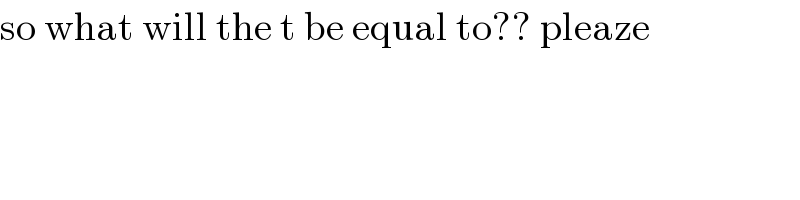
$$\mathrm{so}\:\mathrm{what}\:\mathrm{will}\:\mathrm{the}\:\mathrm{t}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}??\:\mathrm{pleaze} \\ $$
Commented by PRITHWISH SEN 2 last updated on 06/Jul/20

$$\frac{\mathrm{7}}{\mathrm{2}}\:\mathrm{for}\:\mathrm{1}^{\mathrm{st}} \\ $$$$\mathrm{and}\:\mathrm{3}\:\mathrm{for}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \\ $$
Commented by pete last updated on 07/Jul/20

$$\mathrm{thank}\:\mathrm{u}\:\mathrm{sir} \\ $$
