Question Number 30613 by NECx last updated on 23/Feb/18

Commented by NECx last updated on 24/Feb/18

Answered by mrW2 last updated on 25/Feb/18

Commented by NECx last updated on 25/Feb/18

Commented by mrW2 last updated on 25/Feb/18

Commented by mrW2 last updated on 25/Feb/18

Commented by mrW2 last updated on 25/Feb/18
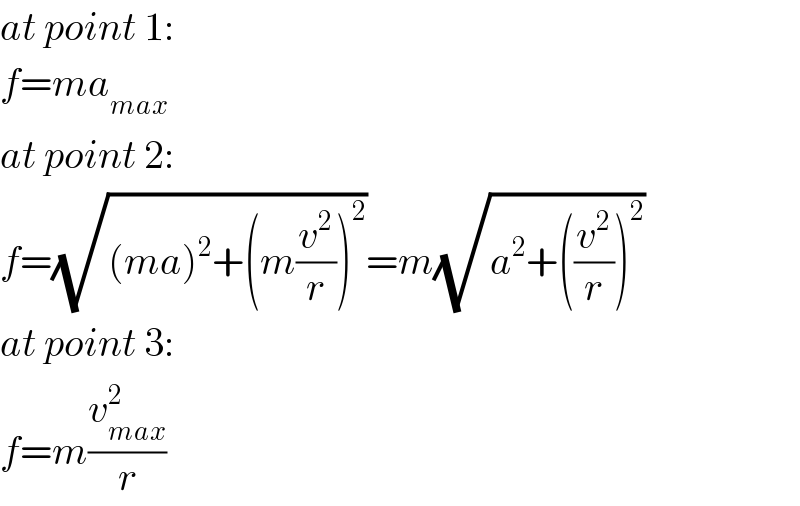
Commented by NECx last updated on 25/Feb/18

Commented by mrW2 last updated on 27/Feb/18

Commented by NECx last updated on 06/Mar/18

